Posted on

Building a Distributed Log from Scratch, Part 3: Scaling Message Delivery

In part two of this series we discussed data replication within the context of a distributed log and how it relates to high availability. Next, we’ll look at what it takes to scale the log such that it can handle non-trivial workloads.

Data Scalability

A key part of scaling any kind of data-intensive system is the ability to partition the data. Partitioning is how we can scale a system linearly, that is to say we can handle more load by adding more nodes. We make the system horizontally scalable.

Kafka was designed this way from the beginning. Topics are partitioned and ordering is only guaranteed within a partition. For example, in an e-commerce application, we might have two topics, purchases and inventory, each with two partitions. These partitions allow us to distribute reads and writes across a set of brokers. In Kafka, the log is actually the partition.

The challenge with this is how we partition the data. We might distribute data using round robin, in effect randomly distributing it. The problem with this is we lose out on ordering, which is an important characteristic of the log. For example, imagine we have add and remove inventory operations. With random partitioning, we might end up with a remove followed by an add getting processed if they’re placed in different partitions. However, if they’re placed in the same partition, we know they will be ordered correctly from the perspective of the publisher.

We could also distribute by hashing a key and sending all writes with the same keys to the same partitions or some custom partitioning strategy along these lines. Continuing with our example, we might partition purchases by account name and inventory by SKU. This way, all purchase operations by the same account are ordered, as are all inventory operations pertaining to the same SKU. The diagram below shows a (naive) custom strategy that partitions topics by ranges based on the account and SKU.

The important point here is that how you partition your data is largely dependent on your application and its usage patterns, but partitioning is a critical part of scalability. It allows you to scale your workload processing by dividing up responsibilities, which in turn, allows you to throw more resources at the problem in a tractable way.

One of NATS Streaming’s shortcomings, in my opinion, is that it doesn’t currently offer a good story around partitioning. Channels are totally ordered, essentially making them the equivalent of a Kafka partition. The workaround is to partition among multiple channels at the application level. To some, this is a benefit because it’s conceptually simpler than Kafka, but Kafka was designed as such because scalability was a key design goal from day one.

Consumer Scalability

One challenge with the log is the problem of high fan-out. Specifically, how do we scale to a large number of consumers? In Kafka and NATS Streaming, reads (and writes) are only served by the leader. Similarly, Amazon Kinesis supports up to only five reads per second per shard (a shard is Kinesis’ equivalent of a partition). Thus, if we have five consumers reading from the same shard, we’ve already hit our fan-out limit. The thought is to partition your workload to increase parallelism and/or daisy chain streams to increase fan-out. But if we are trying to do very high fan-out, e.g. to thousands of IoT devices, neither of these are ideal solutions. Not all use cases may lend themselves to partitioning (though one can argue this is just a sign of poor architecting), and chaining up streams (or in Kafka nomenclature, topics) tends to be kludgey.

However, we can make the following observation: with an immutable log, there are no stale or phantom reads. Unlike a database, we can loosen our requirements a bit. Whereas a database is typically mutable, with a log, we’re only appending things. From a consumer’s perspective, a replica is either up-to-date with the leader or in the process of catching up, but in either case, if we read all of the records, we should end up in the same state. Immutability, at least in theory, should make it “easy” to scale to a large number of consumers because we don’t have to read from the leader to get correct results (ignoring log compaction and other “mutable” operations), so long as we’re okay with strong eventual consistency with respect to tailing the log.

In NATS Streaming, with Raft, we could simply allow followers to serve reads and scale reads by increasing the size of the cluster, but this would impact performance because the quorum size would also increase. Instead, we can use “non-voters” to act as read replicas and balance consumers among them. These read replicas do not participate in quorum or leader election, they simply receive committed log entries. In effect, this is the daisy chaining of streams mentioned earlier but done implicitly by the system. This is an otherwise common pattern for increasing consumer fan-out in Kinesis but is usually done in an ad hoc, Rube Goldberg-esque fashion. Note that, in the case of NATS Streaming, this isn’t quite as simple as it sounds due to the delivery mechanism used, which we’ll describe next.

Push vs. Pull

In Kafka, consumers pull data from brokers. In NATS Streaming, brokers push data to consumers. Kafka’s documentation describes this design decision in detail. The key factor largely comes down to flow control. With push, flow control needs to be explicit to deal with diverse consumers. Different consumers will consume at different rates, so the broker needs to be aware of this so as not to overwhelm a consumer.

There are obvious advantages and disadvantages to both approaches. With push, it can be a tricky balance to ensure full utilization of the consumer. We might use a backoff protocol like additive increase/multiplicative decrease, widely known for its use in TCP congestion control, to optimize utilization. NATS Streaming, like many other messaging systems, implements flow control by using acks. Upon receiving a message, consumers ack back to the server, and the server tracks the in-flight messages for each consumer. If that number goes above a certain threshold, the server will stop delivery until more acks are received. There is a similar flow-control mechanism between the publisher and the server. The trade-off here is the server needs to do some bookkeeping, which we’ll get to in a bit. With a pull-based system, flow control is implicit. Consumers simply go at their own pace, and the server doesn’t need to track anything. There is much less complexity with this.

Pull-based systems lend themselves to aggressive batching. With push, we must decide whether to send a message immediately or wait to accumulate more messages before sending. This is a decision pertaining to latency versus throughput. Push is often viewed as an optimization for latency, but if we’re tuning for low latency, we send messages one at a time only for them to end up being buffered on the consumer anyway. With pull, the consumer fetches all available messages after its current position in the log, which basically removes the guesswork around tuning batching and latency.

There are API implications with this decision too, particularly from an ergonomics and complexity perspective. Kafka clients tend to be “thick” and have a lot of complexity. That is, they do a lot because the broker is designed to be simple. That’s my guess as to why there are so few native client libraries up to par with the Java client. NATS Streaming clients, on the other hand, are relatively “thin” because the server does more. We end up just pushing the complexity around based on our design decisions, but one can argue that the smart client and dumb server is a more scalable approach. We’ll go into detail on that in the next installment of this series.

Circling back on consumer scalability, the fact that NATS Streaming uses a push-based model means we can’t simply setup read replicas and balance consumers among them. Instead, we would need to partition consumers among the replicas so that each server is responsible for pushing data to a subset of consumers. The increased complexity over pull becomes immediately apparent here.

Bookkeeping

There are two ways to track position in the log: have the server track it for consumers or have consumers track it themselves. Again, there are trade-offs with this, namely between API simplicity, server complexity, performance, and scalability. NATS Streaming tracks subscription positions for consumers. This means consumers can come and go as they like and pick back up where they left off easily. Before NATS Streaming supported clustering, this made a lot of sense because the bookkeeping was all in one server. But with clustering, this data must be replicated just like the message data, which poses a performance challenge.

The alternative is to punt the problem to the consumer. But also keep in mind that consumers might not have access to fast stable storage, such as with an IoT device or ephemeral container. Is there a way we can split the difference?

We can store the offsets themselves directly in the log. As of 0.9, this is what Kafka does. Before that, clients had to manage offsets themselves or store them in ZooKeeper. This forced a dependency on ZooKeeper for clients but also posed a major bottleneck since ZooKeeper is relatively low throughput. But by storing offsets in the log, they are treated just like any other write to a Kafka topic, which scales quite well (offsets are stored in an internal Kafka topic called __consumer_offsets partitioned by consumer group; there is also a special read cache for speeding up the read path).

Clients periodically checkpoint their offset to the log. We then use log compaction to retain only the latest offsets. Log compaction works by rewriting the log to retain only the latest message for a given key. On recovery, clients fetch the latest offset from the log. The important part here is we need to structure our keys such that compaction retains the latest offset for each unique consumer. For example, we might structure it as consumer-topic-partition. We end up with something resembling the following, where the message value is the offset:

The above log is uncompacted. Once compacted, it becomes the following:

Note that compaction violates some of our previous assumptions around the immutability of the log, but that’s for another discussion.

There are a number of advantages to this approach. We get fault-tolerance and durability due to the fact that our log is already fault-tolerant and durable as designed earlier. We get consistent reads again due to our replication scheme. Unlike ZooKeeper, we get high write throughput. And we reuse existing structures, so there’s less server complexity. We’re just reusing the log, there aren’t really any major new codepaths.

Interestingly, the bookkeeping needed for flow control in push-based systems—such as acks in NATS Streaming—serves much the same purpose as offset tracking in pull-based systems, since it needs to track position. The difference comes when we allow out-of-order processing. If we don’t allow it, then acks are simply a high-water mark that indicate the client is “this far” caught up. The problem with push is we also have to deal with redeliveries, whereas with pull they are implicitly handled by the client.  If we do allow out-of-order processing, then we need to track individual, in-flight messages, which is what per-message acks allow us to do. In this case, the system starts to look less like a log and more like a message queue. This makes push even more complicated.

The nice thing about reusing the log to track offsets is it greatly reduces the amount of code and complexity needed. Since NATS Streaming allows out-of-order processing, it uses a separate acking subsystem which otherwise has the same requirements as an offset-tracking subsystem.

In part four of this series, we will discuss some of the key trade-offs involved with implementing a distributed log and some lessons learned while building NATS Streaming.

Posted on

Building a Distributed Log from Scratch, Part 2: Data Replication

In part one of this series we introduced the idea of a message log, touched on why it’s useful, and discussed the storage mechanics behind it. In part two, we discuss data replication.

We have our log. We know how to write data to it and read it back as well as how data is persisted. The caveat to this is, although we have a durable log, it’s a single point of failure (SPOF). If the machine where the log data is stored dies, we’re SOL. Recall that one of our three priorities with this system is high availability, so the question is how do we achieve high availability and fault tolerance?

With high availability, we’re specifically talking about ensuring continuity of reads and writes. A server failing shouldn’t preclude either of these, or at least unavailability should be kept to an absolute minimum and without the need for operator intervention. Ensuring this continuity should be fairly obvious: we eliminate the SPOF. To do that, we replicate the data. Replication can also be a means for increasing scalability, but for now we’re only looking at this through the lens of high availability.

There are a number of ways we can go about replicating the log data. Broadly speaking, we can group the techniques into two different categories: gossip/multicast protocols and consensus protocols. The former includes things like epidemic broadcast trees, bimodal multicast, SWIM, HyParView, and NeEM. These tend to be eventually consistent and/or stochastic. The latter, which I’ve described in more detail here, includes 2PC/3PC, Paxos, Raft, Zab, and chain replication. These tend to favor strong consistency over availability.

So there are a lot of ways we can replicate data, but some of these solutions are better suited than others to this particular problem. Since ordering is an important property of a log, consistency becomes important for a replicated log. If we read from one replica and then read from another, it’s important those views of the log don’t conflict with each other. This more or less rules out the stochastic and eventually consistent options, leaving us with consensus-based replication.

There are essentially two components to consensus-based replication schemes: 1) designate a leader who is responsible for sequencing writes and 2) replicate the writes to the rest of the cluster.

Designating a leader can be as simple as a configuration setting, but the purpose of replication is fault tolerance. If our configured leader crashes, we’re no longer able to accept writes. This means we need the leader to be dynamic. It turns out leader election is a well-understood problem, so we’ll get to this in a bit.

Once a leader is established, it needs to replicate the data to followers. In general, this can be done by either waiting for all replicas or waiting for only a quorum (majority) of replicas. There are pros and cons to both approaches.

Pros Cons
All Replicas Tolerates f failures with f+1 replicas Latency pegged to slowest replica
Quorum Hides delay from a slow replica Tolerates f failures with 2f+1 replicas

Waiting on all replicas means we can make progress as long as at least one replica is available. With quorum, tolerating the same amount of failures requires more replicas because we need a majority to make progress. The trade-off is that the quorum hides any delays from a slow replica. Kafka is an example of a system which uses all replicas (with some conditions on this which we will see later), and NATS Streaming is one that uses a quorum. Let’s take a look at both in more detail.

Replication in Kafka

In Kafka, a leader is selected (we’ll touch on this in a moment). This leader maintains an in-sync replica set (ISR) consisting of all the replicas which are fully caught up with the leader. This is every replica, by definition, at the beginning. All reads and writes go through the leader. The leader writes messages to a write-ahead log (WAL). Messages written to the WAL are considered uncommitted or “dirty” initially. The leader only commits a message once all replicas in the ISR have written it to their own WAL. The leader also maintains a high-water mark (HW) which is the last committed message in the WAL. This gets piggybacked on the replica fetch responses from which replicas periodically checkpoint to disk for recovery purposes. The piggybacked HW then allows replicas to know when to commit.

Only committed messages are exposed to consumers. However, producers can configure how they want to receive acknowledgements on writes. It can wait until the message is committed on the leader (and thus replicated to the ISR), wait for the message to only be written (but not committed) to the leader’s WAL, or not wait at all. This all depends on what trade-offs the producer wants to make between latency and durability.

The graphic below shows how this replication process works for a cluster of three brokers: b1, b2, and b3. Followers are effectively special consumers of the leader’s log.

Now let’s look at a few failure modes and how Kafka handles them.

Leader Fails

Kafka relies on Apache ZooKeeper for certain cluster coordination tasks, such as leader election, though this is not actually how the log leader is elected. A Kafka cluster has a single controller broker whose election is handled by ZooKeeper. This controller is responsible for performing administrative tasks on the cluster. One of these tasks is selecting a new log leader (actually partition leader, but this will be described later in the series) from the ISR when the current leader dies. ZooKeeper is also used to detect these broker failures and signal them to the controller.

Thus, when the leader crashes, the cluster controller is notified by ZooKeeper and it selects a new leader from the ISR and announces this to the followers. This gives us automatic failover of the leader. All committed messages up to the HW are preserved and uncommitted messages may be lost during the failover. In this case, b1 fails and b2 steps up as leader.

Follower Fails

The leader tracks information on how “caught up” each replica is. Before Kafka 0.9, this included both how many messages a replica was behind, replica.lag.max.messages, and the amount of time since the replica last fetched messages from the leader, replica.lag.time.max.ms. Since 0.9, replica.lag.max.messages was removed and replica.lag.time.max.ms now refers to both the time since the last fetch request and the amount of time since the replica last caught up.

Thus, when a follower fails (or stops fetching messages for whatever reason), the leader will detect this based on replica.lag.time.max.ms. After that time expires, the leader will consider the replica out of sync and remove it from the ISR. In this scenario, the cluster enters an “under-replicated” state since the ISR has shrunk. Specifically, b2 fails and is removed from the ISR.

Follower Temporarily Partitioned

The case of a follower being temporarily partitioned, e.g. due to a transient network failure, is handled in a similar fashion to the follower itself failing. These two failure modes can really be combined since the latter is just the former with an arbitrarily long partition, i.e. it’s the difference between crash-stop and crash-recovery models.

In this case, b3 is partitioned from the leader. As before, replica.lag.time.max.ms acts as our failure detector and causes b3 to be removed from the ISR. We enter an under-replicated state and the remaining two brokers continue committing messages 4 and 5. Accordingly, the HW is updated to 5 on these brokers.

When the partition heals, b3 continues reading from the leader and catching up. Once it is fully caught up with the leader, it’s added back into the ISR and the cluster resumes its fully replicated state.

We can generalize this to the crash-recovery model. For example, instead of a network partition, the follower could crash and be restarted later. When the failed replica is restarted, it recovers the HW from disk and truncates its log up to the HW. This preserves the invariant that messages after the HW are not guaranteed to be committed. At this point, it can begin catching up from the leader and will end up with a log consistent with the leader’s once fully caught up.

Replication in NATS Streaming

NATS Streaming relies on the Raft consensus algorithm for leader election and data replication. This sometimes comes as a surprise to some as Raft is largely seen as a protocol for replicated state machines. We’ll try to understand why Raft was chosen for this particular problem in the following sections. We won’t dive deep into Raft itself beyond what is needed for the purposes of this discussion.

While a log is a state machine, it’s a very simple one: a series of appends. Raft is frequently used as the replication mechanism for key-value stores which have a clearer notion of “state machine.” For example, with a key-value store, we have set and delete operations. If we set foo = bar and then later set foo = baz, the state gets rolled up. That is, we don’t necessarily care about the provenance of the key, only its current state.

However, NATS Streaming differs from Kafka in a number of key ways. One of these differences is that NATS Streaming attempts to provide a sort of unified API for streaming and queueing semantics not too dissimilar from Apache Pulsar. This means, while it has a notion of a log, it also has subscriptions on that log. Unlike Kafka, NATS Streaming tracks these subscriptions and metadata associated with them, such as where a client is in the log. These have definite “state machines” affiliated with them, like creating and deleting subscriptions, positions in the log, clients joining or leaving queue groups, and message-redelivery information.

Currently, NATS Streaming uses multiple Raft groups for replication. There is a single metadata Raft group used for replicating client state and there is a separate Raft group per topic which replicates messages and subscriptions.

Raft solves both the problems of leader election and data replication in a single protocol. The Secret Lives of Data provides an excellent interactive illustration of how this works. As you step through that illustration, you’ll notice that the algorithm is actually quite similar to the Kafka replication protocol we walked through earlier. This is because although Raft is used to implement replicated state machines, it actually is a replicated WAL, which is exactly what Kafka is. One benefit of using Raft is we no longer have the need for ZooKeeper or some other coordination service.

Raft handles electing a leader. Heartbeats are used to maintain leadership. Writes flow through the leader to the followers. The leader appends writes to its WAL and they are subsequently piggybacked onto the heartbeats which get sent to the followers using AppendEntries messages. At this point, the followers append the write to their own WALs, assuming they don’t detect a gap, and send a response back to the leader. The leader commits the write once it receives a successful response from a quorum of followers.

Similar to Kafka, each replica in Raft maintains a high-water mark of sorts called the commit index, which is the index of the highest log entry known to be committed. This is piggybacked on the AppendEntries messages which the followers use to know when to commit entries in their WALs. If a follower detects that it missed an entry (i.e. there was a gap in the log), it rejects the AppendEntries and informs the leader to rewind the replication. The Raft paper details how it ensures correctness, even in the face of many failure modes such as the ones described earlier.

Conceptually, there are two logs: the Raft log and the NATS Streaming message log. The Raft log handles replicating messages and, once committed, they are appended to the NATS Streaming log. If it seems like there’s some redundancy here, that’s because there is, which we’ll get to soon. However, keep in mind we’re not just replicating the message log, but also the state machines associated with the log and any clients.

There are a few challenges with this replication technique, two of which we will talk about. The first is scaling Raft. With a single topic, there is one Raft group, which means one node is elected leader and it heartbeats messages to followers.

As the number of topics increases, so do the number of Raft groups, each with their own leaders and heartbeats. Unless we constrain the Raft group participants or the number of topics, this creates an explosion of network traffic between nodes.

There are a couple ways we can go about addressing this. One option is to run a fixed number of Raft groups and use a consistent hash to map a topic to a group. This can work well if we know roughly the number of topics beforehand since we can size the number of Raft groups accordingly. If you expect only 10 topics, running 10 Raft groups is probably reasonable. But if you expect 10,000 topics, you probably don’t want 10,000 Raft groups. If hashing is consistent, it would be feasible to dynamically add or remove Raft groups at runtime, but it would still require repartitioning a portion of topics which can be complicated.

Another option is to run an entire node’s worth of topics as a single group using a layer on top of Raft. This is what CockroachDB does to scale Raft in proportion to the number of key ranges using a layer on top of Raft they call MultiRaft. This requires some cooperation from the Raft implementation, so it’s a bit more involved than the partitioning technique but eschews the repartitioning problem and redundant heartbeating.

The second challenge with using Raft for this problem is the issue of “dual writes.” As mentioned before, there are really two logs: the Raft log and the NATS Streaming message log, which we’ll call the “store.” When a message is published, the leader writes it to its Raft log and it goes through the Raft replication process.

Once the message is committed in Raft, it’s written to the NATS Streaming log and the message is now visible to consumers.

Note, however, that not only messages are written to the Raft log. We also have subscriptions and cluster topology changes, for instance. These other items are not written to the NATS Streaming log but handled in other ways on commit. That said, messages tend to occur in much greater volume than these other entries.

Messages end up getting stored redundantly, once in the Raft log and once in the NATS Streaming log. We can address this problem if we think about our logs a bit differently. If you recall from part one, our log storage consists of two parts: the log segment and the log index. The segment stores the actual log data, and the index stores a mapping from log offset to position in the segment.

Along these lines, we can think of the Raft log index as a “physical offset” and the NATS Streaming log index as a “logical offset.” Instead of maintaining two logs, we treat the Raft log as our message write-ahead log and treat the NATS Streaming log as an index into that WAL. Particularly, messages are written to the Raft log as usual. Once committed, we write an index entry for the message offset that points back into the log. As before, we use the index to do lookups into the log and can then read sequentially from the log itself.

Remaining Questions

We’ve answered the questions of how to ensure continuity of reads and writes, how to replicate data, and how to ensure replicas are consistent. The remaining two questions pertaining to replication are how do we keep things fast and how do we ensure data is durable?

There are several things we can do with respect to performance. The first is we can configure publisher acks depending on our application’s requirements. Specifically, we have three options. The first is the broker acks on commit. This is slow but safe as it guarantees the data is replicated. The second is the broker acks on appending to its local log. This is fast but unsafe since it doesn’t wait on any replica roundtrips but, by that very fact, means that the data is not replicated. If the leader crashes, the message could be lost. Lastly, the publisher can just not wait for an ack at all. This is the fastest but least safe option for obvious reasons. Tuning this all depends on what requirements and trade-offs make sense for your application.

The second thing we do is don’t explicitly fsync writes on the broker and instead rely on replication for durability. Both Kafka and NATS Streaming (when clustered) do this. With fsync enabled (in Kafka, this is configured with flush.messages and/or flush.ms and in NATS Streaming, with file_sync), every message that gets published results in a sync to disk. This ends up being very expensive. The thought here is if we are replicating to enough nodes, the replication itself is sufficient for HA of data since the likelihood of more than a quorum of nodes failing is low, especially if we are using rack-aware clustering. Note that data is still periodically flushed in the background by the kernel.

Batching aggressively is also a key part of ensuring good performance. Kafka supports end-to-end batching from the producer all the way to the consumer. NATS Streaming does not currently support batching at the API level, but it uses aggressive batching when replicating and persisting messages. In my experience, this makes about an order-of-magnitude improvement in throughput.

Finally, as already discussed earlier in the series, keeping disk access sequential and maximizing zero-copy reads makes a big difference as well.

There are a few things worth noting with respect to durability. Quorum is what guarantees durability of data. This comes “for free” with Raft due to the nature of that protocol. In Kafka, we need to do a bit of configuring to ensure this. Namely, we need to configure min.insync.replicas on the broker and acks on the producer. The former controls the minimum number of replicas that must acknowledge a write for it to be considered successful when a producer sets acks to “all.” The latter controls the number of acknowledgments the producer requires the leader to have received before considering a request complete. For example, with a topic that has a replication factor of three, min.insync.replicas needs to be set to two and acks set to “all.” This will, in effect, require a quorum of two replicas to process writes.

Another caveat with Kafka is unclean leader elections. That is, if all replicas become unavailable, there are two options: choose the first replica to come back to life (not necessarily in the ISR) and elect this replica as leader (which could result in data loss) or wait for a replica in the ISR to come back to life and elect it as leader (which could result in prolonged unavailability). Initially, Kafka favored availability by default by choosing the first strategy. If you preferred consistency, you needed to set unclean.leader.election.enable to false. However, as of 0.11, unclean.leader.election.enable now defaults to this.

Fundamentally, durability and consistency are at odds with availability. If there is no quorum, then no reads or writes can be accepted and the cluster is unavailable. This is the crux of the CAP theorem.

In part three of this series, we will discuss scaling message delivery in the distributed log.

Posted on

Building a Distributed Log from Scratch, Part 1: Storage Mechanics

The log is a totally-ordered, append-only data structure. It’s a powerful yet simple abstraction—a sequence of immutable events. It’s something that programmers have been using for a very long time, perhaps without even realizing it because it’s so simple. Whether it’s application logs, system logs, or access logs, logging is something every developer uses on a daily basis. Essentially, it’s a timestamp and an event, a when and a what, and typically appended to the end of a file. But when we generalize that pattern, we end up with something much more useful for a broad range of problems. It becomes more interesting when we look at the log not just as a system of record but a central piece in managing data and distributing it across the enterprise efficiently.

 

There are a number of implementations of this idea: Apache Kafka, Amazon Kinesis, NATS Streaming, Tank, and Apache Pulsar to name a few. We can probably credit Kafka with popularizing the idea.

I think there are at least three key priorities for the effectiveness of one of these types of systems: performance, high availability, and scalability. If it’s not fast enough, the data becomes decreasingly useful. If it’s not highly available, it means we can’t reliably get our data in or out. And if it’s not scalable, it won’t be able to meet the needs of many enterprises.

When we apply the traditional pub/sub semantics to this idea of a log, it becomes a very useful abstraction that applies to a lot of different problems.

In this series, we’re not going to spend much time discussing why the log is useful. Jay Kreps has already done the legwork on that with The Log: What every software engineer should know about real-time data’s unifying abstraction. There’s even a book on it. Instead, we will focus on what it takes to build something like this using Kafka and NATS Streaming as case studies of sorts—Kafka because of its ubiquity, NATS Streaming because it’s something with which I have personal experience. We’ll look at a few core components like leader election, data replication, log persistence, and message delivery. Part one of this series starts with the storage mechanics. Along the way, we will also discuss some lessons learned while building NATS Streaming, which is a streaming data layer on top of the NATS messaging system. The intended outcome of this series is threefold: to learn a bit about the internals of a log abstraction, to learn how it can achieve the three goals described above, and to learn some applied distributed systems theory.

With that in mind, you will probably never need to build something like this yourself (nor should you), but it helps to know how it works. I also find that software engineering is all about pattern matching. Many types of problems look radically different but are surprisingly similar. Some of these ideas may apply to other things you come across. If nothing else, it’s just interesting.

Let’s start by looking at data storage since this is a critical part of the log and dictates some other aspects of it. Before we dive into that, though, let’s highlight some first principles we’ll use as a starting point for driving our design.

As we know, the log is an ordered, immutable sequence of messages. Messages are atomic, meaning they can’t be broken up. A message is either in the log or not, all or nothing. Although we only ever add messages to the log and never remove them (as with a message queue), the log has a notion of message retention based on some policies, which allows us to control how the log is truncated. This is a practical requirement since otherwise the log will grow endlessly. These policies might be based on time, number of messages, number of bytes, etc.

The log can be played back from any arbitrary position. With position, we normally refer to a logical message timestamp rather than a physical wall-clock time, such as an offset into the log. The log is stored on disk, and sequential disk access is actually relatively fast. The graphic below taken from the ACM Queue article The Pathologies of Big Data helps bear this out (this is helpfully pointed out by Kafka’s documentation).

That said, modern OS page caches mean that sequential access often avoids going to disk altogether. This is because the kernel keeps cached pages in otherwise unused portions of RAM. This means both reads and writes go to the in-memory page cache instead of disk. With Kafka, for example, we can verify this quite easily by running a simple test that writes some data and reads it back and looking at disk IO using iostat. After running such a test, you will likely see something resembling the following, which shows the number of blocks read and written is exactly zero.

avg-cpu:  %user   %nice %system %iowait  %steal   %idle
          13.53    0.00   11.28    0.00    0.00   75.19

Device:    tps   Blk_read/s   Blk_wrtn/s   Blk_read   Blk_wrtn
xvda      0.00         0.00         0.00          0          0

With the above in mind, our log starts to look an awful lot like an actual logging file, but instead of timestamps and log messages, we have offsets and opaque data messages. We simply add new messages to the end of the file with a monotonically increasing offset.

However, there are some problems with this approach. Namely, the file is going to get very, very large. Recall that we need to support a few different access patterns: looking up messages by offset and also truncating the log using a variety of different retention policies. Since the log is ordered, a lookup is simply a binary search for the offset, but this is expensive with a large log file. Similarly, aging out data by retention policy is harder.

To account for this, we break up the log file into chunks. In Kafka, these are called segments. In NATS Streaming, they are called slices. Each segment is a new file. At a given time, there is a single active segment, which is the segment messages are written to. Once the segment is full (based on some configuration), a new one is created and becomes active.

Segments are defined by their base offset, i.e. the offset of the first message stored in the segment. In Kafka, the files are also named with this offset. This allows us to quickly locate the segment in which a given message is contained by doing a binary search.

Alongside each segment file is an index file that maps message offsets to their respective positions in the log segment. In Kafka, the index uses 4 bytes for storing an offset relative to the base offset and 4 bytes for storing the log position. Using a relative offset is more efficient because it means we can avoid storing the actual offset as an int64. In NATS Streaming, the timestamp is also stored to do time-based lookups.

Ideally, the data written to the log segment is written in protocol format. That is, what gets written to disk is exactly what gets sent over the wire. This allows for zero-copy reads. Let’s take a look at how this otherwise works.

When you read messages from the log, the kernel will attempt to pull the data from the page cache. If it’s not there, it will be read from disk. The data is copied from disk to page cache, which all happens in kernel space. Next, the data is copied into the application (i.e. user space). This all happens with the read system call. Now the application writes the data out to a socket using send, which is going to copy it back into kernel space to a socket buffer before it’s copied one last time to the NIC. All in all, we have four copies (including one from page cache) and two system calls.

However, if the data is already in wire format, we can bypass user space entirely using the sendfile system call, which will copy the data directly from the page cache to the NIC buffer—two copies (including one from page cache) and one system call. This turns out to be an important optimization, especially in garbage-collected languages since we’re bringing less data into application memory. Zero-copy also reduces CPU cycles and memory bandwidth.

NATS Streaming does not currently make use of zero-copy for a number of reasons, some of which we will get into later in the series. In fact, the NATS Streaming storage layer is actually pluggable in that it can be backed by any number of mediums which implement the storage interface. Out of the box it includes the file-backed storage described above, in-memory, and SQL-backed.

There are a few other optimizations to make here such as message batching and compression, but we’ll leave those as an exercise for the reader.

In part two of this series, we will discuss how to make this log fault tolerant by diving into data-replication techniques.

Posted on

Thrift on Steroids: A Tale of Scale and Abstraction

Apache Thrift is an RPC framework developed at Facebook for building “scalable cross-language services.” It consists of an interface definition language (IDL), communication protocol, API libraries, and a code generator that allows you to build and evolve services independently and in a polyglot fashion across a wide range of languages. This is nothing new and has been around for over a decade now.

There are a number of notable users of Thrift aside from Facebook, including Twitter (mainly by way of Finagle), Foursquare, Pinterest, Uber (via TChannel), and Evernote, among others—and for good reason, Thrift is mature and battle-tested.

The white paper explains the motivation behind Thrift in greater detail, though I think the following paragraph taken from the introduction does a pretty good job of summarizing it:

As Facebook’s traffic and network structure have scaled, the resource demands of many operations on the site (i.e. search, ad selection and delivery, event logging) have presented technical requirements drastically outside the scope of the LAMP framework. In our implementation of these services, various programming languages have been selected to optimize for the right combination of performance, ease and speed of development, availability of existing libraries, etc. By and large, Facebook’s engineering culture has tended towards choosing the best tools and implementations available over standardizing on any one programming language and begrudgingly accepting its inherent limitations.

Basically, as Facebook scaled, they moved more and more away from PHP and the LAMP stack and became increasingly polyglot. I think this same evolution is seen at most startups as they grow into themselves. We saw a similar transition in my time at Workiva, moving from our monolothic Python application on Google App Engine to a polyglot service-oriented architecture in AWS. It was an exciting but awkward time as we went through our adolescence as an engineering culture and teams started to find their identities. Teams learned what it meant to build backward-compatible APIs and loosely coupled services, how to deprecate APIs, how to build resilient and highly available systems, how to properly instrument services and diagnose issues, how to run and manage the underlying infrastructure, and—most importantly—how to collaborate with each other. There was lots of stumbling and mistakes along the way, lots of postmortems, lots of stress, but with that comes the learning and growing. The payoff is big but the process is painful. I don’t think it ever isn’t.

With one or two services written in the same language and relatively few developers, it was easy to just stick with “REST” (in quotes because it’s always a bastardized version of what REST ought to be), sling some JSON around, and call it a day. As the number of tech stacks and integration points increase, it becomes apparent that some standards are important. And once things are highly polyglot with lots of developers and lots of services running with lots of versions, strict service contracts become essential.

Uber has a blog post on building microservices that explains this and why they settled on Thrift to solve this problem.

Since the number of service calls grows rapidly, it is necessary to maintain a well-defined interface for every call. We knew we wanted to use an IDL for managing this interface, and we ultimately decided on Thrift. Thrift forces service owners to publish strict interface definitions, which streamlines the process of integrating with services. Calls that do not abide by the interface are rejected at the Thrift level instead of leaking into a service and failing deeper within the code. This strategy of publicly declaring your interface emphasizes the importance of backwards compatibility, since multiple versions of a service’s Thrift interface could be in use at any given time. The service author must not make breaking changes, and instead must only make non-breaking additions to the interface definition until all consumers are ready for deprecation.

Early on, I was tasked with building a unified messaging solution that would help with our integration challenges. The advantages of a unified solution should be obvious: reusability (before this, everyone was solving the problem in their own way), focus (allow developers to focus on their problem space, not the glue), acceleration (if the tools are already available, there’s less work to do), and shared pain points (it’s a lot easier to prioritize your work when everyone is complaining about the same thing). Also, a longer term benefit is developing the knowledge of this shared solution into an organizational competency which has a sort of “economy of scale” to it. Our job was not just to ship a messaging platform but evangelize it and help other teams to be successful with it. We did this through countless blog posts, training sessions, workshops, talks, and even a podcast.

Before we set out on building a common messaging solution, there were a few key principles we used to guide ourselves. We wanted to provide a core set of tools, libraries, and infrastructure for service integration. We wanted a solution that was rigid yet flexible. We provide only a minimal set of messaging patterns to act as generic building blocks with strict, strongly typed APIs, and promote design best practices and a service-oriented mindset. This meant supporting service evolution and API iteration through versioning and backward compatibility, allowing for resiliency patterns like timeouts, retries, circuit breakers, etc., and generally advocating asynchronous, loosely coupled communication. Lastly, we had to keep in mind that, at the end of the day, developers are just trying to ship stuff, so we had to balance these concerns out with ergonomics and developer experience so they could build, integrate, and ship quickly.

As much as I think RPC is a bad abstraction, it’s what developers want. If you don’t provide them with an RPC solution, they will build their own, so we had to provide first-class support for it. We evaluated solutions in the RPC space. We looked at GRPC extensively, which is the new RPC hotness from Google, but it had a few key drawbacks, namely its “newness” (it was still in early beta at the time and has since been almost entirely rewritten), it’s coupled to HTTP/2 as a transport (which at the time had fairly limited support), and it lacks support for JavaScript (let alone Dart, which is what most of our client applications were being written in). Avro was another we looked at.

Ultimately, we settled on Thrift due to its maturity and wide use in production, its performance, its architecture (it separates out the transports, protocols, and RPC layer with the first two being pluggable), its rich feature set, and its wide range of language support (checking off all the languages we standardized on as a company including Go, Java, Python, JavaScript, and Dart). Thrift is not without its problems though—more on this in a bit.

In addition to RPC, we wanted to promote a more asynchronous, message-passing style of communication with pub/sub. This would allow for greater flexibility in messaging patterns like fan-out and fan-in, interest-based messaging, and reduced coupling and fragility of services. This enables things like the worker pattern where we can distribute work to a pool of workers and scale that pool independently, whereas RPC tends to promote more stateful types of services. In my experience, developers tend to bias towards stateful services since this is how we’ve built things for a long time, but as we’ve entered the cloud-native era, things are running in containers which are autoscaled, more ephemeral, and more distributed. We have to grapple with the complexity imposed by distributed systems. This is why asynchronous messaging is important and why we wanted to support it from the onset.

We selected NATS as a messaging backplane because of its simplicity, performance, scalability, and adoption of the cloud-native mentality. When it comes to service integration, you need an always-on dial tone and NATS provides just that. Because of Thrift’s pluggable transport layer, we could build a NATS RPC transport while also providing HTTP and TCP transports.

Unfortunately, Thrift doesn’t provide any kind of support for pub/sub, and we wanted the same guarantees for it that we had with RPC, like type safety and versioning with code-generated APIs and service contracts. Aside from this, Thrift has a number of other, more glaring problems:

  • Head-of-line blocking: a single, slow request will block any subsequent requests for a client.
  • Out-of-order responses: an out-of-order response puts a Thrift transport in a bad state, requiring it to be torn down and reestablished, e.g. if a slow request times out at the client, the client issues a subsequent request, and a response comes back for the first request, the client blows up.
  • Concurrency: a Thrift client cannot be shared between multiple threads of execution, requiring each thread to have its own client issuing requests sequentially. This, combined with head-of-line blocking, is a major performance killer. This problem is compounded when each transport has its own resources, such as a socket.
  • RPC timeouts: Thrift does not provide good facilities for per-request timeouts, instead opting for a global transport read timeout.
  • Request headers: Thrift does not provide support for request metadata, making it difficult to implement things like authentication/authorization and distributed tracing. Instead, you are required to bake these things into your IDL or in a wrapped transport. The problem with this is it puts the onus on service providers rather than allowing an API gateway or middleware to perform these functions in a centralized way.
  • Middleware: Thrift does not have any support for client or server middleware. This means clients must be wrapped to implement interceptor logic and middleware code must be duplicated within handler functions. This makes it impossible to implement AOP-style logic in a clean, DRY way.

Twitter’s Finagle addresses many of these issues but is solely for the JVM, so we decided to address Thrift’s shortcomings in a cross-platform way without completely reinventing the wheel. That is, we took Thrift and extended it. What we ended up with was Frugal, a superset of Thrift recently open sourced that aims to solve the problems described above while also providing support for asynchronous pub/sub APIs—a sort of Thrift on steroids as I’ve come to call it. Its key features include:

  • Request multiplexing: client requests are fully multiplexed, allowing them to be issued concurrently while simultaneously avoiding the head-of-line blocking and out-of-order response problems. This also lays some groundwork for asynchronous messaging patterns.
  • Thread-safety: clients can be safely shared between multiple threads in which requests can be made in parallel.
  • Pub/sub: IDL and code-generation extensions for defining pub/sub APIs in a type-safe way.
  • Request context: a first-class request context object is added to every operation which allows defining request/response headers and per-request timeouts. By making the context part of the Frugal protocol, headers can be introspected or even injected by external middleware. This context could be used to send OAuth2 tokens and user-context information, avoiding the need to include it everywhere in your IDL and handler logic. Correlation IDs for distributed tracing purposes are also built into the request context.
  • Middleware: client- and server- side middleware is supported for RPC and pub/sub APIs. This allows you to implement interceptor logic around handler functions, e.g. for authentication, logging, or retry policies. One can easily integrate OpenTracing as a middleware, for example.
  • Cross-language: support for Go, Java, Dart, and Python (2.7 and 3.5).

Frugal adds a second kind of transport alongside Thrift’s RPC transport for pub/sub. With this, we provide a NATS transport for both pub/sub and RPC (internally, Workiva also has an at-least-once delivery pub/sub transport built around Amazon SQS for mission-critical data). In addition to this, we built a SDK which developers use to connect to the messaging infrastructure (such as NATS) with minimal ceremony. The messaging SDK played a vital role not just in making it easy for developers to adopt and integrate, but providing us a shim where we could introduce sweeping changes across the organization in one place, such as adding instrumentation, tracing, and authentication. This enabled us to roll critical integration components out to every service by making a change in one place.

To support pub/sub, we extended the Thrift IDL with an additional top-level construct called a scope, which is effectively a pub/sub namespace (basically what a service is to RPC). We wrote the IDL using a parsing expression grammar which allows us to generate a parser. We then implemented a code generator for the various language targets. The Frugal compiler is written in Go and is, at least in my opinion, much more maintainable than Thrift’s C++ codebase. However, the language libraries make use of the existing Thrift APIs, such as protocols, transports, etc. This means we didn’t need to implement any of the low-level mechanics like serialization.

I’ve since left Workiva (and am now actually working on NATS), but as far as I know, Frugal helps power nearly every production service at the company. It was an interesting experience from which I learned a lot. I was happy to see some of that work open sourced so others could use it and learn from it.

Of course, if I were starting over today, things would probably look different. GRPC is much more mature and the notion of a “service mesh” has taken the container world by storm with things like Istio, Linkerd, and Envoy. What we built was Workiva’s service mesh, we just didn’t have a name for it, so we called it a “Messaging SDK.” The corollary to this is you don’t need to adopt bleeding-edge tech to be successful. The concepts are what’s important, and if enough people are working on the same types of problems in parallel, they will likely converge on solutions that look very similar to each other given enough time and enough people working on them.

I think there’s a delicate balance between providing solutions that are “easy” from a developer point of view but may provide longer term drawbacks when it comes to building complex systems the “right” way. I see RPC as an example of this. It’s an “easy” abstraction but it hides a lot of complexity. Service meshes might even be in this category, but they have obvious upsides when it comes to building software in a way that is scalable. Peter Alvaro’s Strange Loop talk “I See What You Mean” does a great job of articulating this dilemma, which I’ve also written about myself. In the end, we decided to optimize for shipping, but we took a principled approach: provide the tools developers need (or want) but help educate them to utilize those tools in a way that allows them to ship products that are reliable and maintainable. Throwing tools or code over the wall is not enough.

Posted on

From the Ground Up: Reasoning About Distributed Systems in the Real World

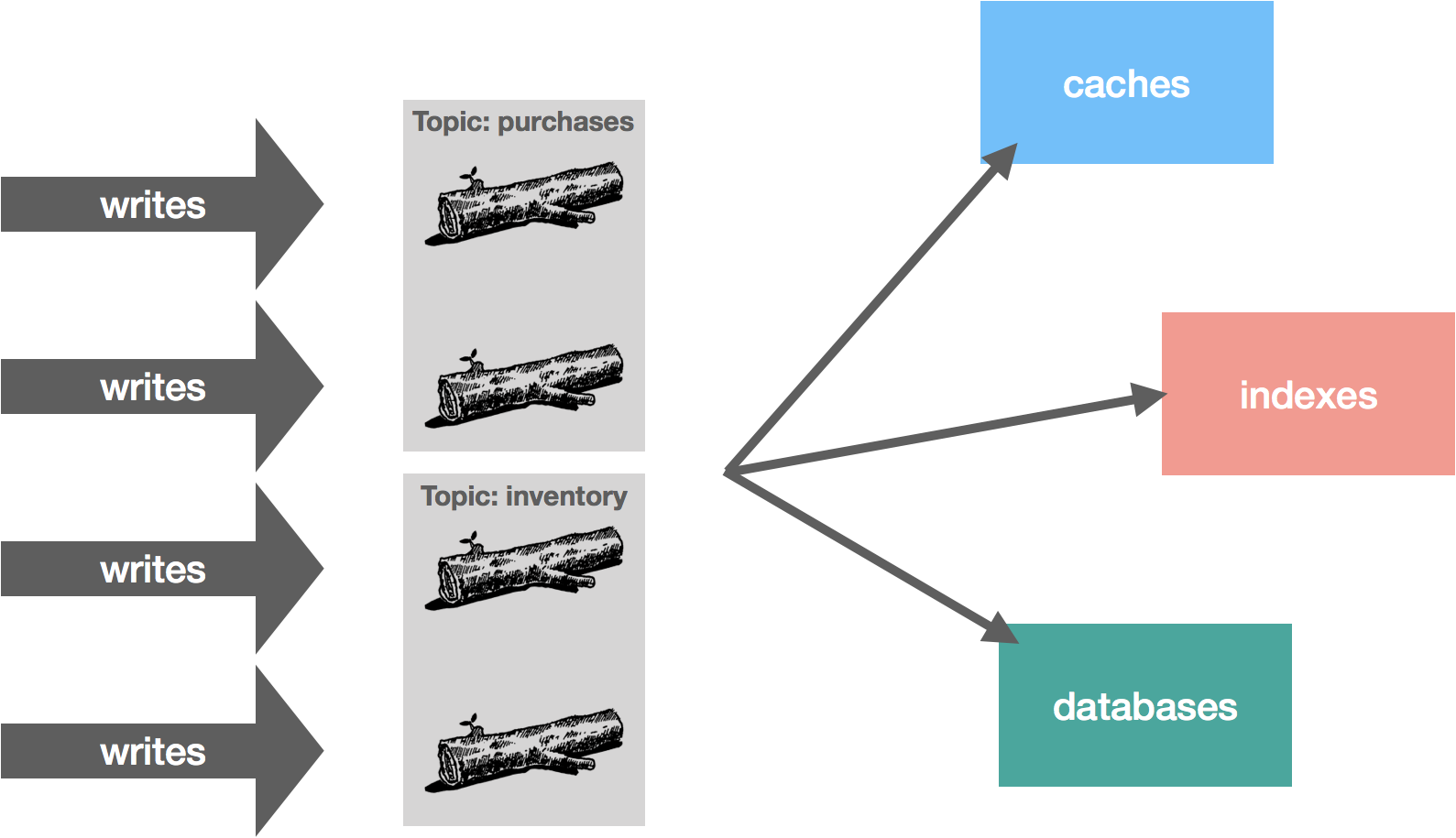
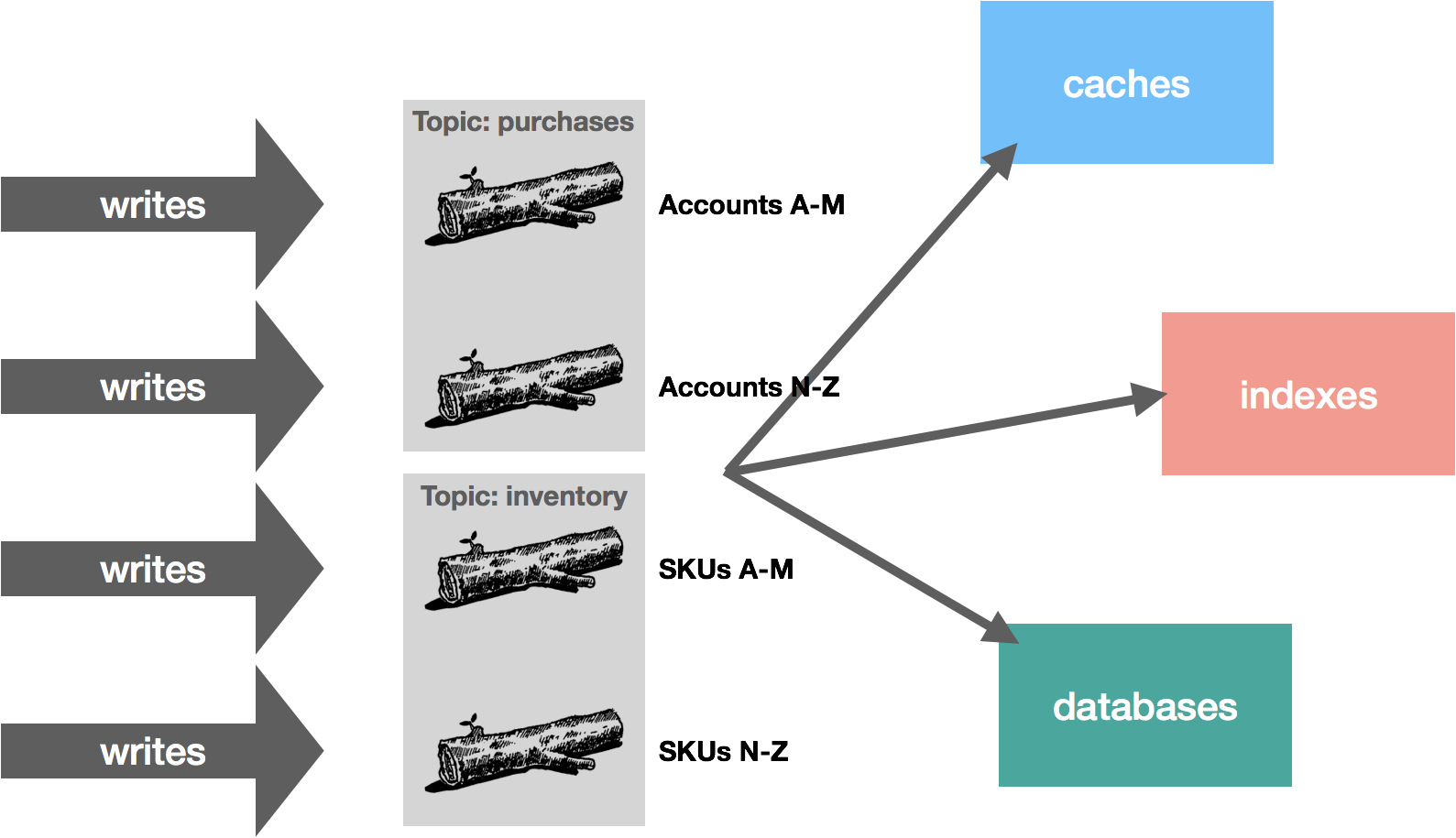
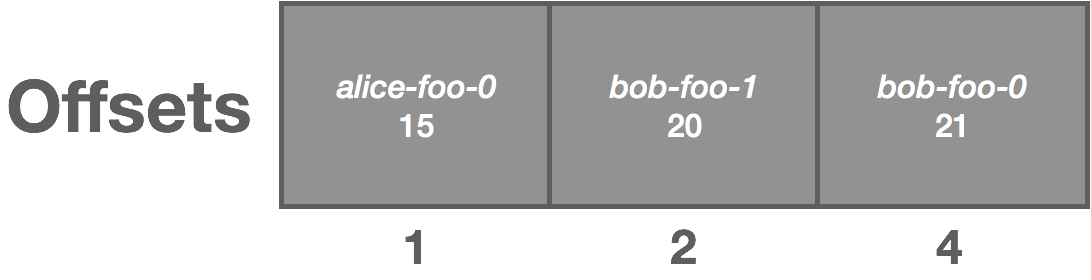
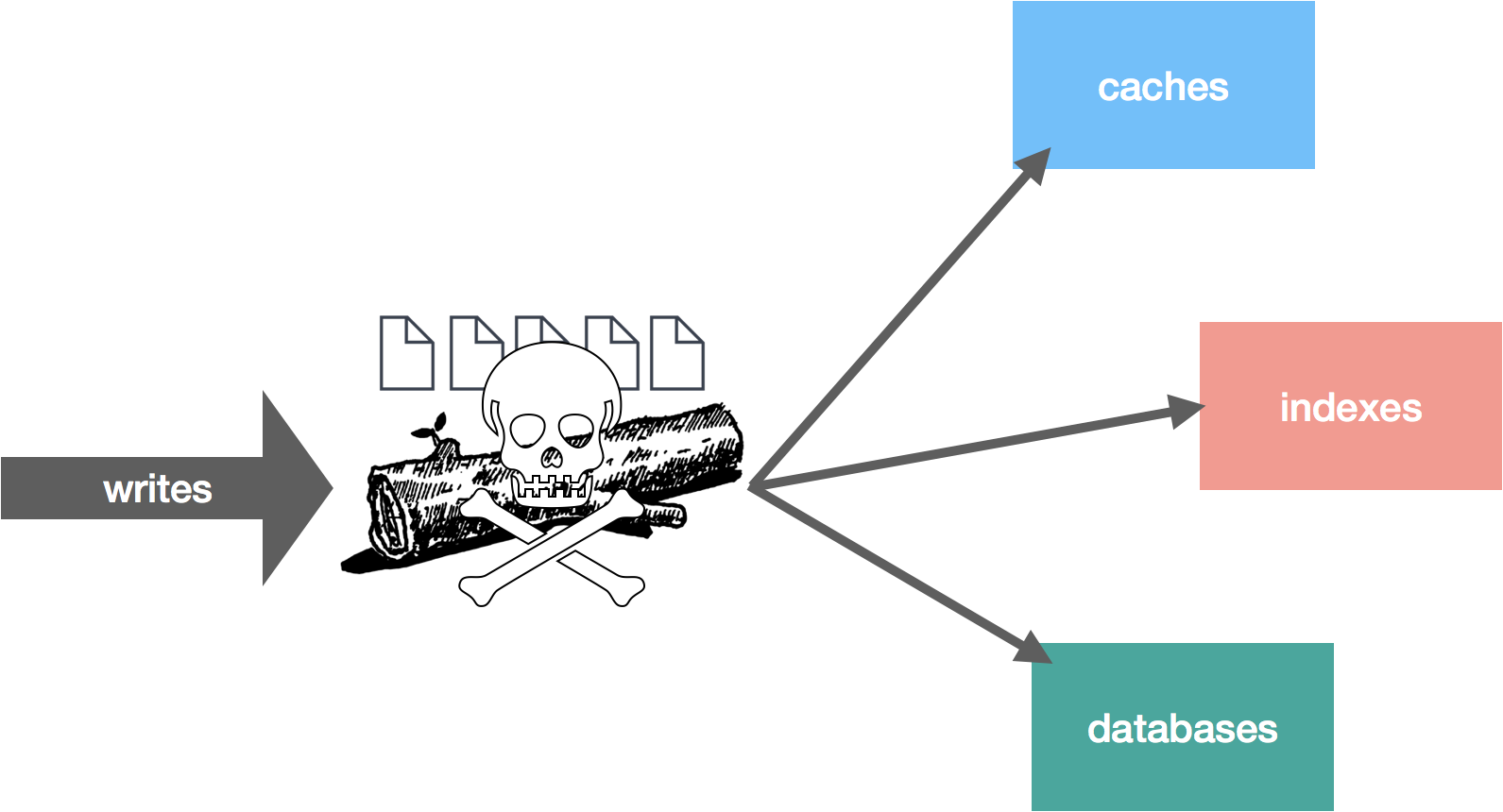
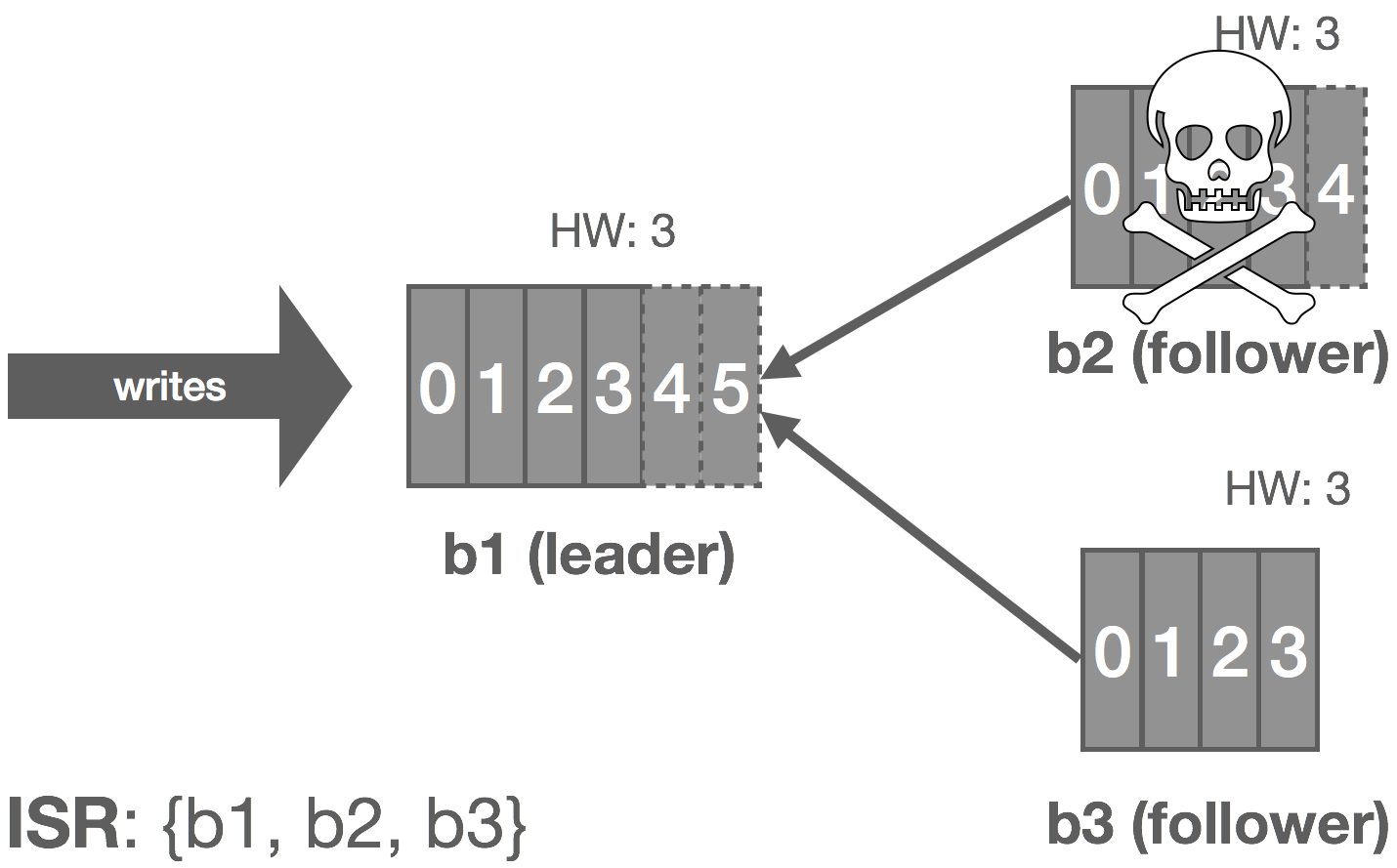
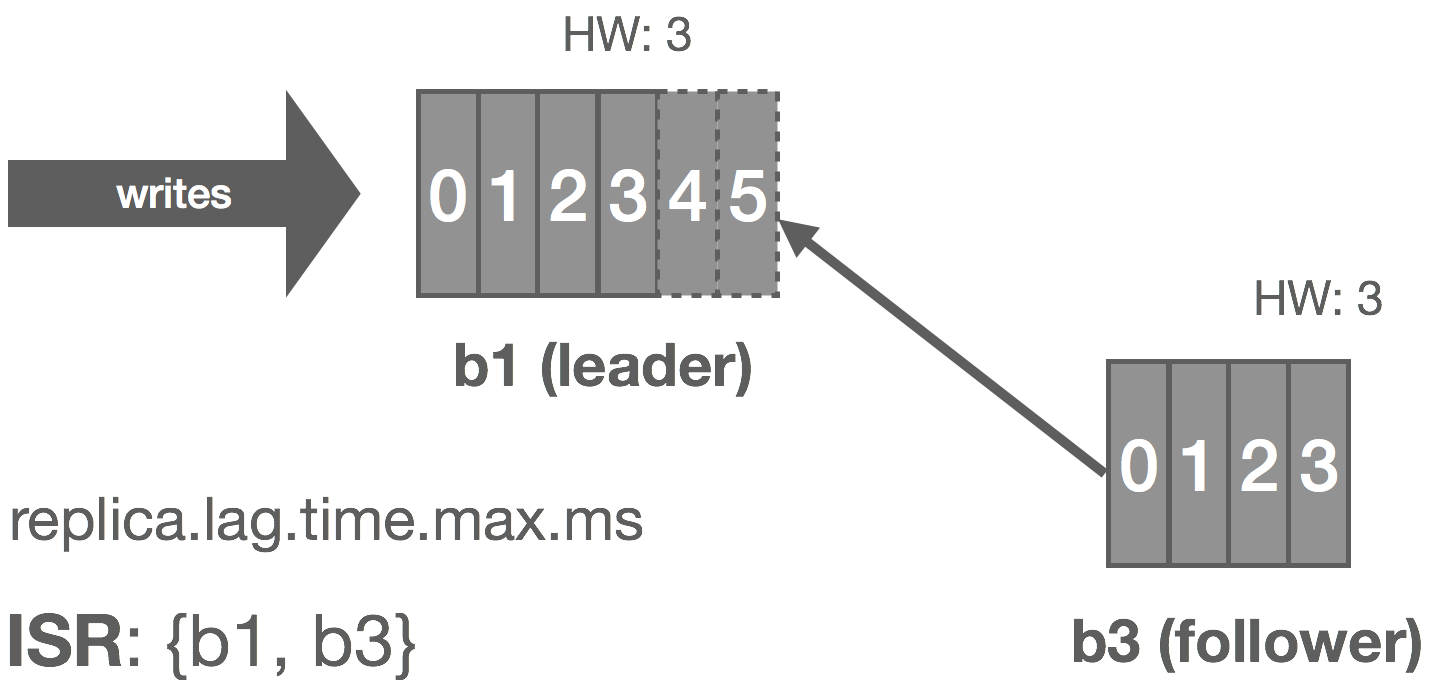
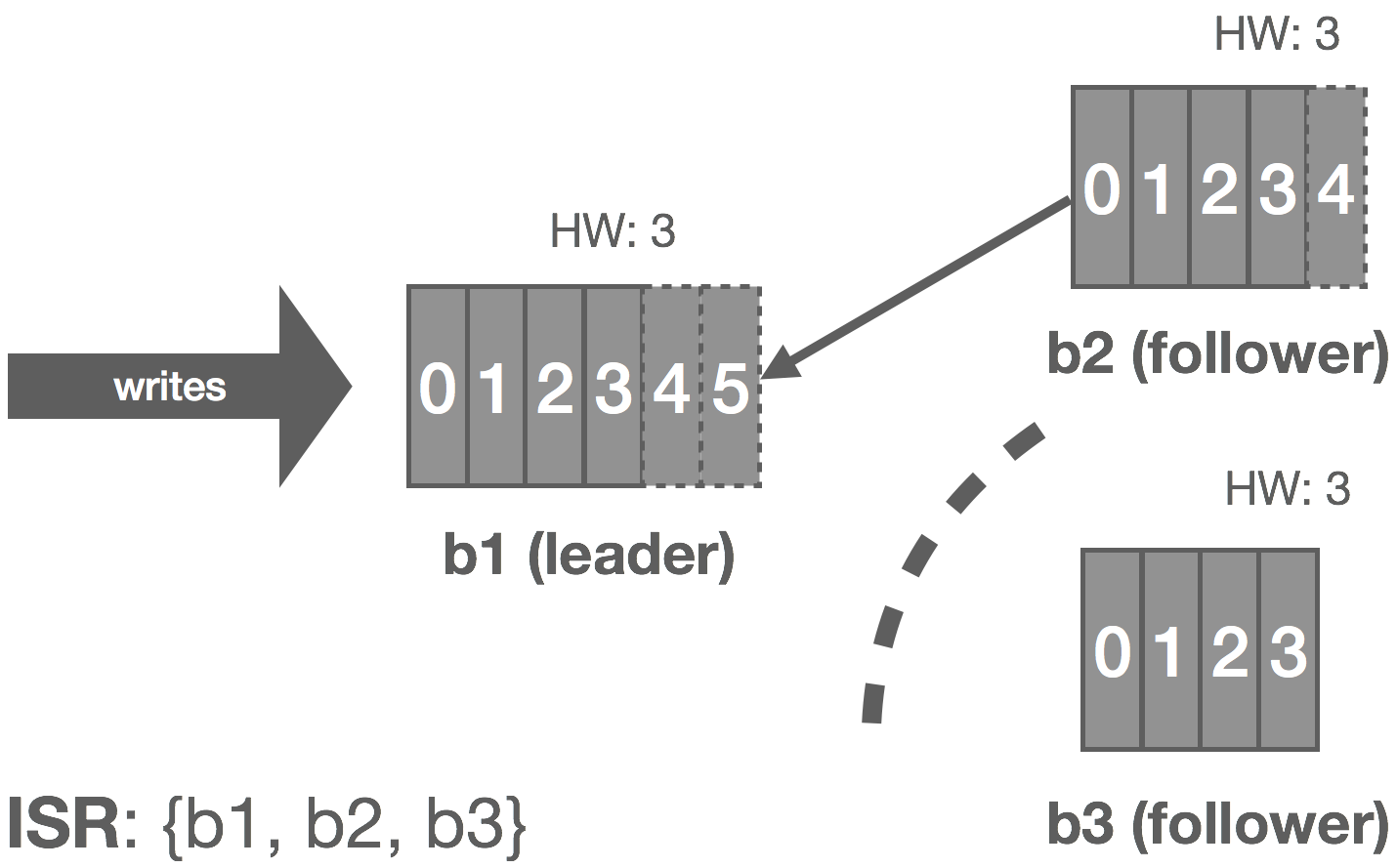
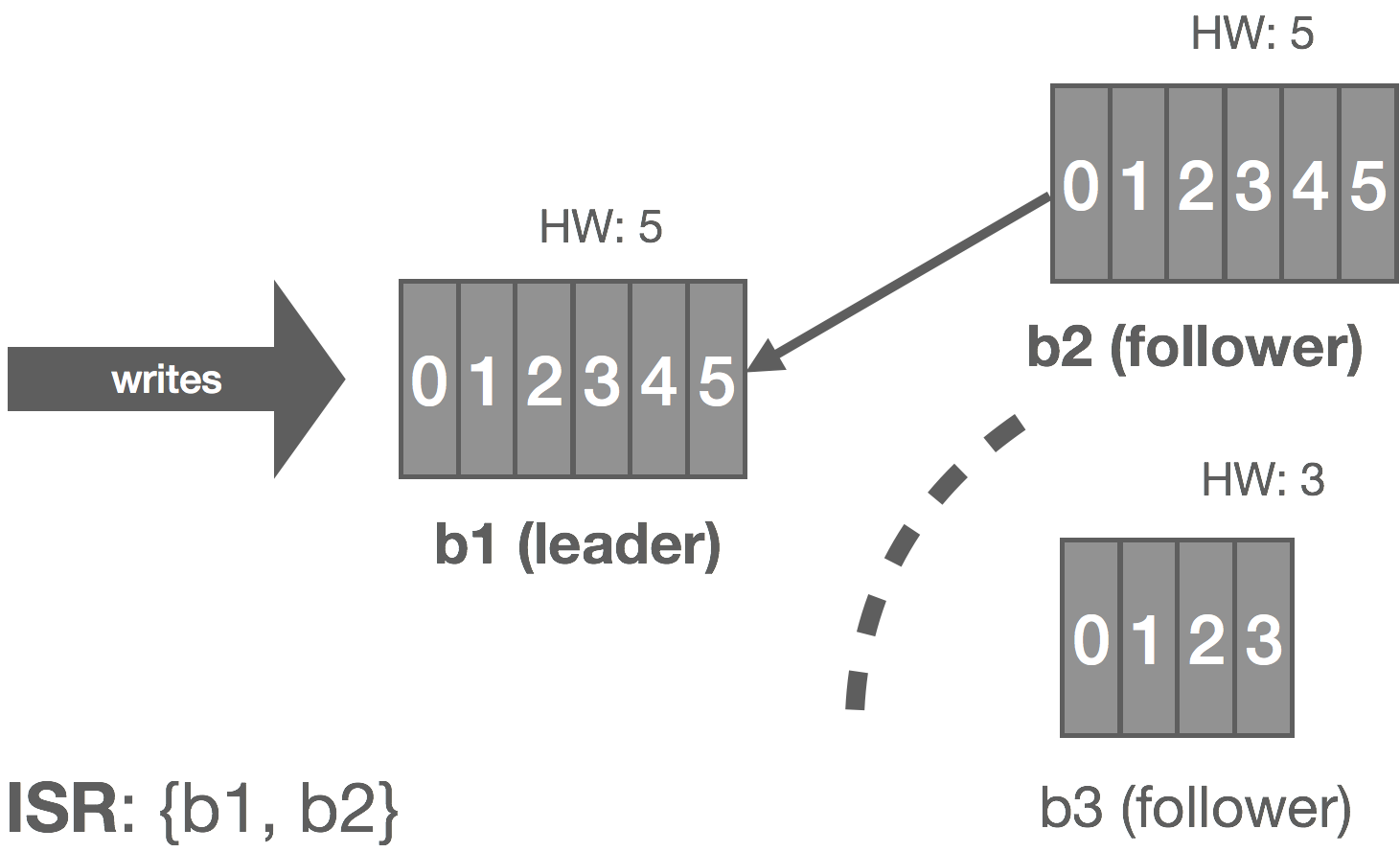
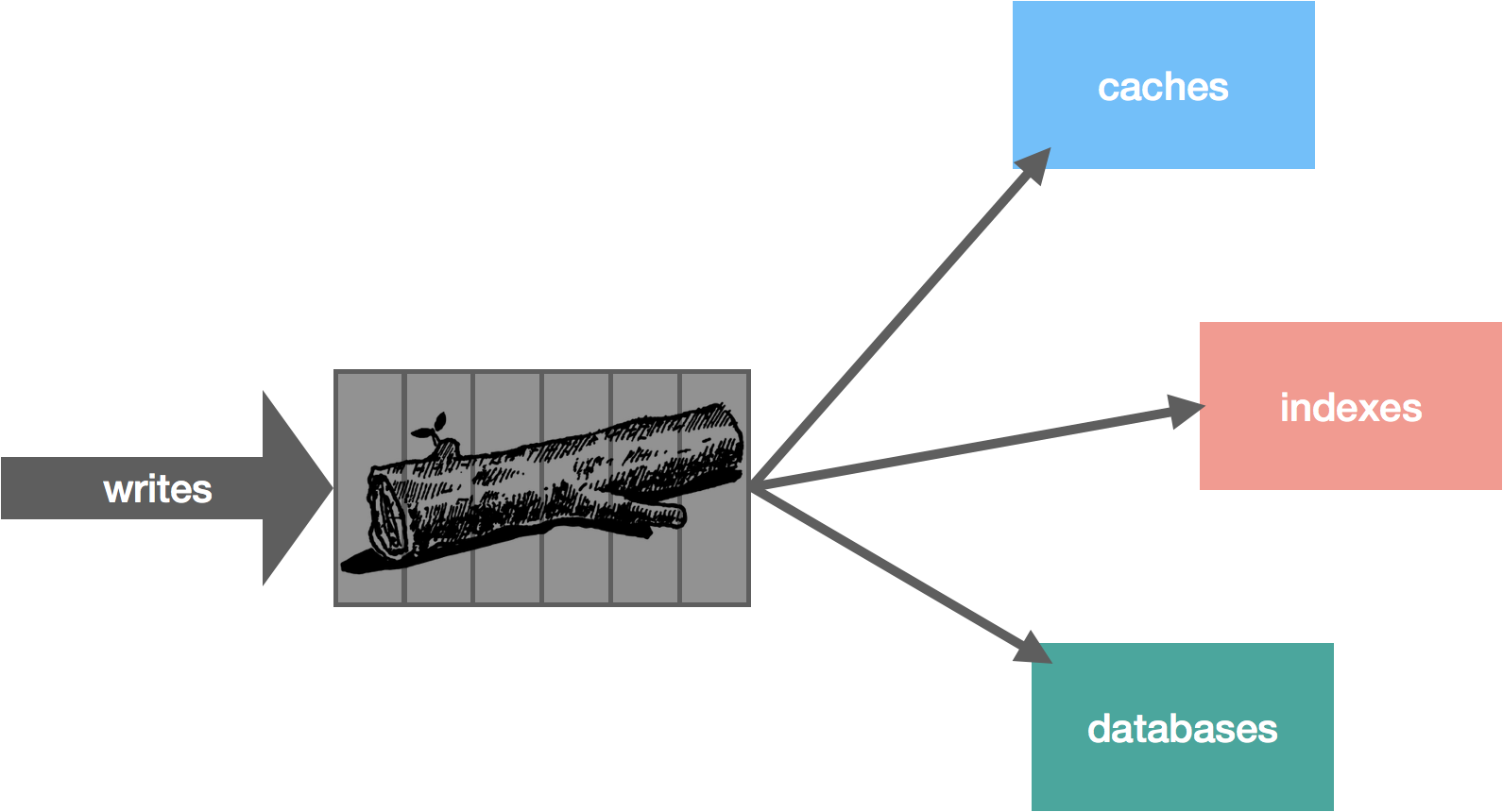
The rabbit hole is deep. Down and down it goes. Where it ends, nobody knows. But as we traverse it, patterns appear. They give us hope, they quell the fear.

Distributed systems literature is abundant, but as a practitioner, I often find it difficult to know where to start or how to synthesize this knowledge without a more formal background. This is a non-academic’s attempt to provide a line of thought for rationalizing design decisions. This piece doesn’t necessarily contribute any new ideas but rather tries to provide a holistic framework by studying some influential existing ones. It includes references which provide a good starting point for thinking about distributed systems. Specifically, we look at a few formal results and slightly less formal design principles to provide a basis from which we can argue about system design.

This is your last chance. After this, there is no turning back. I wish I could say there is no red-pill/blue-pill scenario at play here, but the world of distributed systems is complex. In order to make sense of it, we reason from the ground up while simultaneously stumbling down the deep and cavernous rabbit hole.

Guiding Principles

In order to reason about distributed system design, it’s important to lay out some guiding principles or theorems used to establish an argument. Perhaps the most fundamental of which is the Two Generals Problem originally introduced by Akkoyunlu et al. in Some Constraints and Trade-offs in the Design of Network Communications and popularized by Jim Gray in Notes on Data Base Operating Systems in 1975 and 1978, respectively. The Two Generals Problem demonstrates that it’s impossible for two processes to agree on a decision over an unreliable network. It’s closely related to the binary consensus problem (“attack” or “don’t attack”) where the following conditions must hold:

  • Termination: all correct processes decide some value (liveness property).
  • Validity: if all correct processes decide v, then v must have been proposed by some correct process (non-triviality property).
  • Integrity: all correct processes decide at most one value v, and v is the “right” value (safety property).
  • Agreement: all correct processes must agree on the same value (safety property).

It becomes quickly apparent that any useful distributed algorithm consists of some intersection of both liveness and safety properties. The problem becomes more complicated when we consider an asynchronous network with crash failures:

  • Asynchronous: messages may be delayed arbitrarily long but will eventually be delivered.
  • Crash failure: processes can halt indefinitely.

Considering this environment actually leads us to what is arguably one of the most important results in distributed systems theory: the FLP impossibility result introduced by Fischer, Lynch, and Patterson in their 1985 paper Impossibility of Distributed Consensus with One Faulty Process. This result shows that the Two Generals Problem is provably impossible. When we do not consider an upper bound on the time a process takes to complete its work and respond in a crash-failure model, it’s impossible to make the distinction between a process that is crashed and one that is taking a long time to respond. FLP shows there is no algorithm which deterministically solves the consensus problem in an asynchronous environment when it’s possible for at least one process to crash. Equivalently, we say it’s impossible to have a perfect failure detector in an asynchronous system with crash failures.

When talking about fault-tolerant systems, it’s also important to consider Byzantine faults, which are essentially arbitrary faults. These include, but are not limited to, attacks which might try to subvert the system. For example, a security attack might try to generate or falsify messages. The Byzantine Generals Problem is a generalized version of the Two Generals Problem which describes this fault model. Byzantine fault tolerance attempts to protect against these threats by detecting or masking a bounded number of Byzantine faults.

Why do we care about consensus? The reason is it’s central to so many important problems in system design. Leader election implements consensus allowing you to dynamically promote a coordinator to avoid single points of failure. Distributed databases implement consensus to ensure data consistency across nodes. Message queues implement consensus to provide transactional or ordered delivery. Distributed init systems implement consensus to coordinate processes. Consensus is fundamentally an important problem in distributed programming.

It has been shown time and time again that networks, whether local-area or wide-area, are often unreliable and largely asynchronous. As a result, these proofs impose real and significant challenges to system design.

The implications of these results are not simply academic: these impossibility results have motivated a proliferation of systems and designs offering a range of alternative guarantees in the event of network failures.

L. Peter Deutsch’s fallacies of distributed computing are a key jumping-off point in the theory of distributed systems. It presents a set of incorrect assumptions which many new to the space frequently make, of which the first is “the network is reliable.”

  1. The network is reliable.
  2. Latency is zero.
  3. Bandwidth is infinite.
  4. The network is secure.
  5. Topology doesn’t change.
  6. There is one administrator.
  7. Transport cost is zero.
  8. The network is homogeneous.

The CAP theorem, while recently the subject of scrutiny and debate over whether it’s overstated or not, is a useful tool for establishing fundamental trade-offs in distributed systems and detecting vendor sleight of hand. Gilbert and Lynch’s Perspectives on the CAP Theorem lays out the intrinsic trade-off between safety and liveness in a fault-prone system, while Fox and Brewer’s Harvest, Yield, and Scalable Tolerant Systems characterizes it in a more pragmatic light. I will continue to say unequivocally that the CAP theorem is important within the field of distributed systems and of significance to system designers and practitioners.

A Renewed Hope

Following from the results detailed earlier would imply many distributed algorithms, including those which implement linearizable operations, serializable transactions, and leader election, are a hopeless endeavor. Is it game over? Fortunately, no. Carefully designed distributed systems can maintain correctness without relying on pure coincidence.

First, it’s important to point out that the FLP result does not indicate consensus is unreachable, just that it’s not always reachable in bounded time. Second, the system model FLP uses is, in some ways, a pathological one. Synchronous systems place a known upper bound on message delivery between processes and on process computation. Asynchronous systems have no fixed upper bounds. In practice, systems tend to exhibit partial synchrony, which is described as one of two models by Dwork and Lynch in Consensus in the Presence of Partial Synchrony. In the first model of partial synchrony, fixed bounds exist but they are not known a priori. In the second model, the bounds are known but are only guaranteed to hold starting at unknown time T. Dwork and Lynch present fault-tolerant consensus protocols for both partial-synchrony models combined with various fault models.

Chandra and Toueg introduce the concept of unreliable failure detectors in Unreliable Failure Detectors for Reliable Distributed Systems. Each process has a local, external failure detector which can make mistakes. The detector monitors a subset of the processes in the system and maintains a list of those it suspects to have crashed. Failures are detected by simply pinging each process periodically and suspecting any process which doesn’t respond to the ping within twice the maximum round-trip time for any previous ping. The detector makes a mistake when it erroneously suspects a correct process, but it may later correct the mistake by removing the process from its list of suspects. The presence of failure detectors, even unreliable ones, makes consensus solvable in a slightly relaxed system model.

While consensus ensures processes agree on a value, atomic broadcast ensures processes deliver the same messages in the same order. This same paper shows that the problems of consensus and atomic broadcast are reducible to each other, meaning they are equivalent. Thus, the FLP result and others apply equally to atomic broadcast, which is used in coordination services like Apache ZooKeeper.

In Introduction to Reliable and Secure Distributed Programming, Cachin, Guerraoui, and Rodrigues suggest most practical systems can be described as partially synchronous:

Generally, distributed systems appear to be synchronous. More precisely, for most systems that we know of, it is relatively easy to define physical time bounds that are respected most of the time. There are, however, periods where the timing assumptions do not hold, i.e., periods during which the system is asynchronous. These are periods where the network is overloaded, for instance, or some process has a shortage of memory that slows it down. Typically, the buffer that a process uses to store incoming and outgoing messages may overflow, and messages may thus get lost, violating the time bound on the delivery. The retransmission of the messages may help ensure the reliability of the communication links but introduce unpredictable delays. In this sense, practical systems are partially synchronous.

We capture partial synchrony by assuming timing assumptions only hold eventually without stating exactly when. Similarly, we call the system eventually synchronous. However, this does not guarantee the system is synchronous forever after a certain time, nor does it require the system to be initially asynchronous then after a period of time become synchronous. Instead it implies the system has periods of asynchrony which are not bounded, but there are periods where the system is synchronous long enough for an algorithm to do something useful or terminate. The key thing to remember with asynchronous systems is that they contain no timing assumptions.

Lastly, On the Minimal Synchronism Needed for Distributed Consensus by Dolev, Dwork, and Stockmeyer describes a consensus protocol as t-resilient if it operates correctly when at most t processes fail. In the paper, several critical system parameters and synchronicity conditions are identified, and it’s shown how varying them affects the t-resiliency of an algorithm. Consensus is shown to be provably possible for some models and impossible for others.

Fault-tolerant consensus is made possible by relying on quorums. The intuition is that as long as a majority of processes agree on every decision, there is at least one process which knows about the complete history in the presence of faults.

Deterministic consensus, and by extension a number of other useful algorithms, is impossible in certain system models, but we can model most real-world systems in a way that circumvents this. Nevertheless, it shows the inherent complexities involved with distributed systems and the rigor needed to solve certain problems.

Theory to Practice

What does all of this mean for us in practice? For starters, it means distributed systems are usually a harder problem than they let on. Unfortunately, this is often the cause of improperly documented trade-offs or, in many cases, data loss and safety violations. It also suggests we need to rethink the way we design systems by shifting the focus from system properties and guarantees to business rules and application invariants.

One of my favorite papers is End-To-End Arguments in System Design by Saltzer, Reed, and Clark. It’s an easy read, but it presents a compelling design principle for determining where to place functionality in a distributed system. The principle idea behind the end-to-end argument is that functions placed at a low level in a system may be redundant or of little value when compared to the cost of providing them at that low level. It follows that, in many situations, it makes more sense to flip guarantees “inside out”—pushing them outwards rather than relying on subsystems, middleware, or low-level layers of the stack to maintain them.

To illustrate this, we consider the problem of “careful file transfer.” A file is stored by a file system on the disk of computer A, which is linked by a communication network to computer B. The goal is to move the file from computer A’s storage to computer B’s storage without damage and in the face of various failures along the way. The application in this case is the file-transfer program which relies on storage and network abstractions. We can enumerate just a few of the potential problems an application designer might be concerned with:

  1. The file, though originally written correctly onto the disk at host A, if read now may contain incorrect data, perhaps because of hardware faults in the disk storage system.
  2. The software of the file system, the file transfer program, or the data communication system might make a mistake in buffering and copying the data of the file, either at host A or host B.
  3. The hardware processor or its local memory might have a transient error while doing the buffering and copying, either at host A or host B.
  4. The communication system might drop or change the bits in a packet, or lose a packet or deliver a packet more than once.
  5. Either of the hosts may crash part way through the transaction after performing an unknown amount (perhaps all) of the transaction.

Many of these problems are Byzantine in nature. When we consider each threat one by one, it becomes abundantly clear that even if we place countermeasures in the low-level subsystems, there will still be checks required in the high-level application. For example, we might place checksums, retries, and sequencing of packets in the communication system to provide reliable data transmission, but this really only eliminates threat four. An end-to-end checksum and retry mechanism at the file-transfer level is needed to guard against the remaining threats.

Building reliability into the low level has a number of costs involved. It takes a non-trivial amount of effort to build it. It’s redundant and, in fact, hinders performance by reducing the frequency of application retries and adding unneeded overhead. It also has no actual effect on correctness because correctness is determined and enforced by the end-to-end checksum and retries. The reliability and correctness of the communication system is of little importance, so going out of its way to ensure resiliency does not reduce any burden on the application. In fact, ensuring correctness by relying on the low level might be altogether impossible since threat number two requires writing correct programs, but not all programs involved may be written by the file-transfer application programmer.

Fundamentally, there are two problems with placing functionality at the lower level. First, the lower level is not aware of the application needs or semantics, which means logic placed there is often insufficient. This leads to duplication of logic as seen in the example earlier. Second, other applications which rely on the lower level pay the cost of the added functionality even when they don’t necessarily need it.

Saltzer, Reed, and Clark propose the end-to-end principle as a sort of “Occam’s razor” for system design, arguing that it helps guide the placement of functionality and organization of layers in a system.

Because the communication subsystem is frequently specified before applications that use the subsystem are known, the designer may be tempted to “help” the users by taking on more function than necessary. Awareness of end-to end arguments can help to reduce such temptations.

However, it’s important to note that the end-to-end principle is not a panacea. Rather, it’s a guideline to help get designers to think about their solutions end to end, acknowledge their application requirements, and consider their failure modes. Ultimately, it provides a rationale for moving function upward in a layered system, closer to the application that uses the function, but there are always exceptions to the rule. Low-level mechanisms might be built as a performance optimization. Regardless, the end-to-end argument contends that lower levels should avoid taking on any more responsibility than necessary. The “lessons” section from Google’s Bigtable paper echoes some of these same sentiments:

Another lesson we learned is that it is important to delay adding new features until it is clear how the new features will be used. For example, we initially planned to support general-purpose transactions in our API. Because we did not have an immediate use for them, however, we did not implement them. Now that we have many real applications running on Bigtable, we have been able to examine their actual needs, and have discovered that most applications require only single-row transactions. Where people have requested distributed transactions, the most important use is for maintaining secondary indices, and we plan to add a specialized mechanism to satisfy this need. The new mechanism will be less general than distributed transactions, but will be more efficient (especially for updates that span hundreds of rows or more) and will also interact better with our scheme for optimistic cross-datacenter replication.

We’ll see the end-to-end argument as a common theme throughout the remainder of this piece.

Whose Guarantee Is It Anyway?

Generally, we rely on robust algorithms, transaction managers, and coordination services to maintain consistency and application correctness. The problem with these is twofold: they are often unreliable and they impose a massive performance bottleneck.

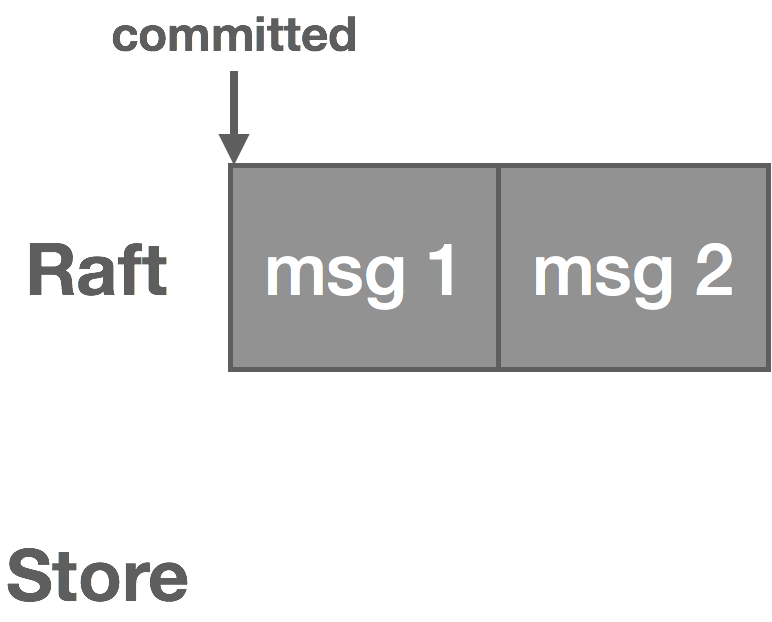
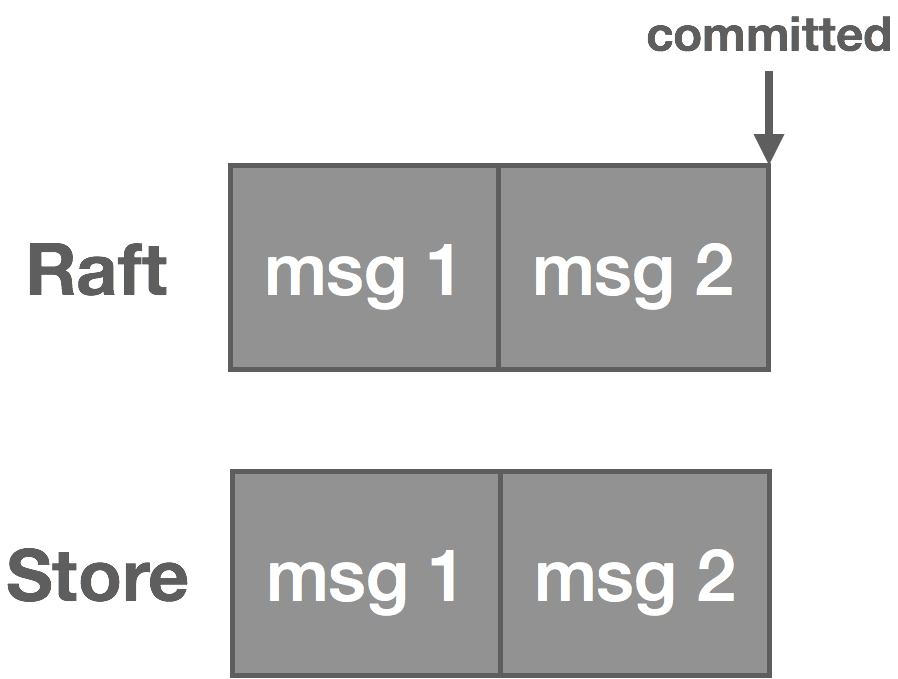
Distributed coordination algorithms are difficult to get right. Even tried-and-true protocols like two-phase commit are susceptible to crash failures and network partitions. Protocols which are more fault tolerant like Paxos and Raft generally don’t scale well beyond small clusters or across wide-area networks. Consensus systems like ZooKeeper own your availability, meaning if you depend on one and it goes down, you’re up a creek. Since quorums are often kept small for performance reasons, this might be less rare than you think.

Coordination systems become a fragile and complex piece of your infrastructure, which seems ironic considering they are usually employed to reduce fragility. On the other hand, message-oriented middleware largely use coordination to provide developers with strong guarantees: exactly-once, ordered, transactional delivery and the like.

From transmission protocols to enterprise message brokers, relying on delivery guarantees is an anti-pattern in distributed system design. Delivery semantics are a tricky business. As such, when it comes to distributed messaging, what you want is often not what you need. It’s important to look at the trade-offs involved, how they impact system design (and UX!), and how we can cope with them to make better decisions.

Subtle and not-so-subtle failure modes make providing strong guarantees exceedingly difficult. In fact, some guarantees, like exactly-once delivery, aren’t even really possible to achieve when we consider things like the Two Generals Problem and the FLP result. When we try to provide semantics like guaranteed, exactly-once, and ordered message delivery, we usually end up with something that’s over-engineered, difficult to deploy and operate, fragile, and slow. What is the upside to all of this? Something that makes your life easier as a developer when things go perfectly well, but the reality is things don’t go perfectly well most of the time. Instead, you end up getting paged at 1 a.m. trying to figure out why RabbitMQ told your monitoring everything is awesome while proceeding to take a dump in your front yard.

If you have something that relies on these types of guarantees in production, know that this will happen to you at least once sooner or later (and probably much more than that). Eventually, a guarantee is going to break down. It might be inconsequential, it might not. Not only is this a precarious way to go about designing things, but if you operate at a large scale, care about throughput, or have sensitive SLAs, it’s probably a nonstarter.

The performance implications of distributed transactions are obvious. Coordination is expensive because processes can’t make progress independently, which in turn limits throughput, availability, and scalability. Peter Bailis gave an excellent talk called Silence is Golden: Coordination-Avoiding Systems Design which explains this in great detail and how coordination can be avoided. In it, he explains how distributed transactions can result in nearly a 400x decrease in throughput in certain situations.

Avoiding coordination enables infinite scale-out while drastically improving throughput and availability, but in some cases coordination is unavoidable. In Coordination Avoidance in Database Systems, Bailis et al. answer a key question: when is coordination necessary for correctness? They present a property, invariant confluence (I-confluence), which is necessary and sufficient for safe, coordination-free, available, and convergent execution. I-confluence essentially works by pushing invariants up into the business layer where we specify correctness in terms of application semantics rather than low-level database operations.

Without knowledge of what “correctness” means to your app (e.g., the invariants used in I-confluence), the best you can do to preserve correctness under a read/write model is serializability.

I-confluence can be determined given a set of transactions and a merge function used to reconcile divergent states. If I-confluence holds, there exists a coordination-free execution strategy that preserves invariants. If it doesn’t hold, no such strategy exists—coordination is required. I-confluence allows us to identify when we can and can’t give up coordination, and by pushing invariants up, we remove a lot of potential bottlenecks from areas which don’t require it.

If we recall, “synchrony” within the context of distributed computing is really just making assumptions about time, so synchronization is basically two or more processes coordinating around time. As we saw, a system which performs no coordination will have optimal performance and availability since everyone can proceed independently. However, a distributed system which performs zero coordination isn’t particularly useful or possible as I-confluence shows. Christopher Meiklejohn’s Strange Loop talk, Distributed, Eventually Consistent Computations, provides an interesting take on coordination with the parable of the car. A car requires friction to drive, but that friction is limited to very small contact points. Any other friction on the car causes problems or inefficiencies. If we think about physical time as friction, we know we can’t eliminate it altogether because it’s essential to the problem, but we want to reduce the use of it in our systems as much as possible. We can typically avoid relying on physical time by instead using logical time, for example, with the use of Lamport clocks or other conflict-resolution techniques. Lamport’s Time, Clocks, and the Ordering of Events in a Distributed System is the classical introduction to this idea.

Often, systems simply forgo coordination altogether for latency-sensitive operations, a perfectly reasonable thing to do provided the trade-off is explicit and well-documented. Sadly, this is frequently not the case. But we can do better. I-confluence provides a useful framework for avoiding coordination, but there’s a seemingly larger lesson to be learned here. What it really advocates is reexamining how we design systems, which seems in some ways to closely parallel our end-to-end argument.

When we think low level, we pay the upfront cost of entry—serializable transactions, linearizable reads and writes, coordination. This seems contradictory to the end-to-end principle. Our application doesn’t really care about atomicity or isolation levels or linearizability. It cares about two users sharing the same ID or two reservations booking the same room or a negative balance in a bank account, but the database doesn’t know that. Sometimes these rules don’t even require any expensive coordination.

If all we do is code our business rules and constraints into the language our infrastructure understands, we end up with a few problems. First, we have to know how to translate our application semantics into these low-level operations while avoiding any impedance mismatch. In the context of messaging, guaranteed delivery doesn’t really mean anything to our application which cares about what’s done with the messages. Second, we preclude ourselves from using a lot of generalized solutions and, in some cases, we end up having to engineer specialized ones ourselves. It’s not clear how well this scales in practice. Third, we pay a performance penalty that could otherwise be avoided (as I-confluence shows). Lastly, we put ourselves at the mercy of our infrastructure and hope it makes good on its promises—it often doesn’t.

Working on a messaging platform team, I’ve had countless conversations which resemble the following exchange:

Developer: “We need fast messaging.”
Me: “Is it okay if messages get dropped occasionally?”
Developer: “What? Of course not! We need it to be reliable.”
Me: “Okay, we’ll add a delivery ack, but what happens if your application crashes before it processes the message?”
Developer: “We’ll ack after processing.”
Me: “What happens if you crash after processing but before acking?”
Developer: “We’ll just retry.”
Me: “So duplicate delivery is okay?”
Developer: “Well, it should really be exactly-once.”
Me: “But you want it to be fast?”
Developer: “Yep. Oh, and it should maintain message ordering.”
Me: “Here’s TCP.”

If, instead, we reevaluate the interactions between our systems, their APIs, their semantics, and move some of that responsibility off of our infrastructure and onto our applications, then maybe we can start to build more robust, resilient, and performant systems. With messaging, does our infrastructure really need to enforce FIFO ordering? Preserving order with distributed messaging in the presence of failure while trying to simultaneously maintain high availability is difficult and expensive. Why rely on it when it can be avoided with commutativity? Likewise, transactional delivery requires coordination which is slow and brittle while still not providing application guarantees. Why rely on it when it can be avoided with idempotence and retries? If you need application-level guarantees, build them into the application level. The infrastructure can’t provide it.

I really like Gregor Hohpe’s “Your Coffee Shop Doesn’t Use Two-Phase Commit” because it shows how simple solutions can be if we just model them off of the real world. It gives me hope we can design better systems, sometimes by just turning things on their head. There’s usually a reason things work the way they do, and it often doesn’t even involve the use of computers or complicated algorithms.

Rather than try to hide complexities by using flaky and heavy abstractions, we should engage directly by recognizing them in our design decisions and thinking end to end. It may be a long and winding path to distributed systems zen, but the best place to start is from the beginning.

I’d like to thank Tom Santero for reviewing an early draft of this writing. Any inaccuracies or opinions expressed are mine alone.