Posted on

Fast Topic Matching

A common problem in messaging middleware is that of efficiently matching message topics with interested subscribers. For example, assume we have a set of subscribers, numbered 1 to 3:

Subscriber Match Request
1 forex.usd
2 forex.*
3 stock.nasdaq.msft

And we have a stream of messages, numbered 1 to N:

Message Topic
1 forex.gbp
2 stock.nyse.ibm
3 stock.nyse.ge
4 forex.eur
5 forex.usd
… …
N stock.nasdaq.msft

We are then tasked with routing messages whose topics match the respective subscriber requests, where a “*” wildcard matches any word. This is frequently a bottleneck for message-oriented middleware like ZeroMQ, RabbitMQ, ActiveMQ, TIBCO EMS, et al. Because of this, there are a number of well-known solutions to the problem. In this post, I’ll describe some of these solutions, as well as a novel one, and attempt to quantify them through benchmarking. As usual, the code is available on GitHub.

The Naive Solution

The naive solution is pretty simple: use a hashmap that maps topics to subscribers. Subscribing involves adding a new entry to the map (or appending to a list if it already exists). Matching a message to subscribers involves scanning through every entry in the map, checking if the match request matches the message topic, and returning the subscribers for those that do.

Inserts are approximately O(1) and lookups approximately O(n*m) where n is the number of subscriptions and m is the number of words in a topic. This means the performance of this solution is heavily dependent upon how many subscriptions exist in the map and also the access patterns (rate of reads vs. writes). Since most use cases are heavily biased towards searches rather than updates, the naive solution—unsurprisingly—is not a great option.

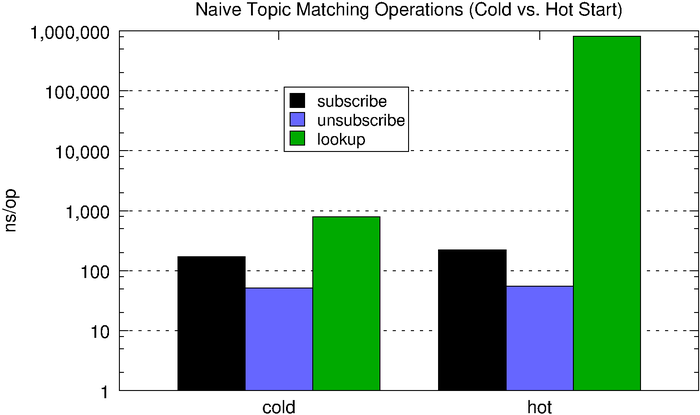
The microbenchmark below compares the performance of subscribe, unsubscribe, and lookup (matching) operations, first using an empty hashmap (what we call cold) and then with one containing 1,000 randomly generated 5-word topic subscriptions (what we call hot). With the populated subscription map, lookups are about three orders of magnitude slower, which is why we have to use a log scale in the chart below.

subscribe unsubscribe lookup
cold 172ns 51.2ns 787ns
hot 221ns 55ns 815,787ns


Inverted Bitmap

The inverted bitmap technique builds on the observation that lookups are more frequent than updates and assumes that the search space is finite. Consequently, it shifts some of the cost from the read path to the write path. It works by storing a set of bitmaps, one per topic, or criteria, in the search space. Subscriptions are then assigned an increasing number starting at 0. We analyze each subscription to determine the matching criteria and set the corresponding bits in the criteria bitmaps to 1. For example, assume our search space consists of the following set of topics:

  • forex.usd
  • forex.gbp
  • forex.jpy
  • forex.eur
  • stock.nasdaq
  • stock.nyse

We then have the following subscriptions:

  • 0 = forex.* (matches forex.usd, forex.gbp, forex.jpy, and forex.eur)
  • 1 = stock.nyse (matches stock.nyse)
  • 2 = *.* (matches everything)
  • 3 = stock.* (matches stock.nasdaq and stock.nyse)

When we index the subscriptions above, we get the following set of bitmaps:

 Criteria 0 1 2 3
forex.usd 1 0 1 0
forex.gbp 1 0 1 0
forex.jpy 1 0 1 0
forex.eur 1 0 1 0
stock.nasdaq 0 0 1 1
stock.nyse 0 1 1 1

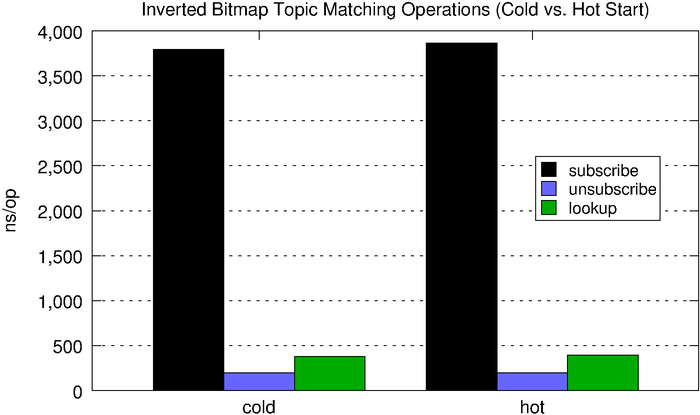
When we match a message, we simply need to lookup the corresponding bitmap and check the set bits. As we see below, subscribe and unsubscribe are quite expensive with respect to the naive solution, but lookups now fall well below half a microsecond, which is pretty good (the fact that the chart below doesn’t use a log scale like the one above should be an indictment of the naive hashmap-based solution).

subscribe unsubscribe lookup
cold 3,795ns 198ns 380ns
hot 3,863ns 198ns 395ns

The inverted bitmap is a better option than the hashmap when we have a read-heavy workload. One limitation is it requires us to know the search space ahead of time or otherwise requires reindexing which, frankly, is prohibitively expensive.

Optimized Inverted Bitmap

The inverted bitmap technique works well enough, but only if the topic space is fairly static. It also falls over pretty quickly when the topic space and number of subscriptions are large, say, millions of topics and thousands of subscribers. The main benefit of topic-based routing is it allows for faster matching algorithms in contrast to content-based routing, which can be exponentially slower. The truth is, to be useful, your topics probably consist of stock.nyse.ibm, stock.nyse.ge, stock.nasdaq.msft, stock.nasdaq.aapl, etc., not stock.nyse and stock.nasdaq. We could end up with an explosion of topics and, even with efficient bitmaps, the memory consumption tends to be too high despite the fact that most of the bitmaps are quite sparse.

Fortunately, we can reduce the amount of memory we consume using a fairly straightforward optimization. Rather than requiring the entire search space a priori, we simply require the max topic size, in terms of words, e.g. stock.nyse.ibm has a size of 3. We can handle topics of the max size or less, e.g. stock.nyse.bac, stock.nasdaq.txn, forex.usd, index, etc. If we see a message with more words than the max, we can safely assume there are no matching subscriptions.

The optimized inverted bitmap works by splitting topics into their constituent parts. Each constituent position has a set of bitmaps, and we use a technique similar to the one described above on each part. We end up with a bitmap for each constituent which we perform a logical AND on to give a resulting bitmap. Each 1 in the resulting bitmap corresponds to a subscription. This means if the max topic size is n, we only AND at most n bitmaps. Furthermore, if we come across any empty bitmaps, we can stop early since we know there are no matching subscribers.

Let’s say our max topic size is 2 and we have the following subscriptions:

  • 0 = forex.*
  • 1 = stock.nyse
  • 2 = index
  • 3 = stock.*

The inverted bitmap for the first constituent looks like the following:

forex.* stock.nyse index stock.*
null 0 0 0 0
forex 1 0 0 0
stock 0 1 0 1
index 0 0 1 0
other 0 0 0 0

And the second constituent bitmap:

forex.* stock.nyse index stock.*
null 0 0 1 0
nyse 0 1 0 0
other 1 0 0 1

The “null” and “other” rows are worth pointing out. “Null” simply means the topic has no corresponding constituent.  For example, “index” has no second constituent, so “null” is marked. “Other” allows us to limit the number of rows needed such that we only need the ones that appear in subscriptions.  For example, if messages are published on forex.eur, forex.usd, and forex.gbp but I merely subscribe to forex.*, there’s no need to index eur, usd, or gbp. Instead, we just mark the “other” row which will match all of them.

Let’s look at an example using the above bitmaps. Imagine we want to route a message published on forex.eur. We split the topic into its constituents: “forex” and “eur.” We get the row corresponding to “forex” from the first constituent bitmap, the one corresponding to “eur” from the second (other), and then AND the rows.

forex.* stock.nyse index stock.*
1 = forex 1 0 0 0
2 = other 1 0 0 1
AND 1 0 0 0

The forex.* subscription matches.

Let’s try one more example: a message published on stock.nyse.

forex.* stock.nyse index stock.*
1 = stock 0 1 0 1
2 = nyse 0 1 0 1
AND 0 1 0 1

In this case, we also need to OR the “other” row for the second constituent. This gives us a match for stock.nyse and stock.*.

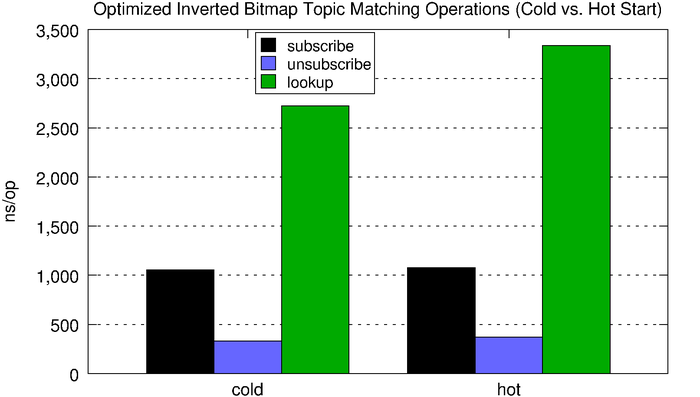
Subscribe operations are significantly faster with the space-optimized inverted bitmap compared to the normal inverted bitmap, but lookups are much slower. However, the optimized version consumes roughly 4.5x less memory for every subscription. The increased flexibility and improved scalability makes the optimized version a better choice for all but the very latency-sensitive use cases.

subscribe unsubscribe lookup
cold 1,053ns 330ns 2,724ns
hot 1,076ns 371ns 3,337ns

Trie

The optimized inverted bitmap improves space complexity, but it does so at the cost of lookup efficiency. Is there a way we can reconcile both time and space complexity? While inverted bitmaps allow for efficient lookups, they are quite wasteful for sparse sets, even when using highly compressed bitmaps like Roaring bitmaps.

Tries can often be more space efficient in these circumstances. When we add a subscription, we descend the trie, adding nodes along the way as necessary, until we run out of words in the topic. Finally, we add some metadata containing the subscription information to the last node in the chain. To match a message topic, we perform a similar traversal. If a node doesn’t exist in the chain, we know there are no subscribers. One downside of this method is, in order to support wildcards, we must backtrack on a literal match and check the “*” branch as well.

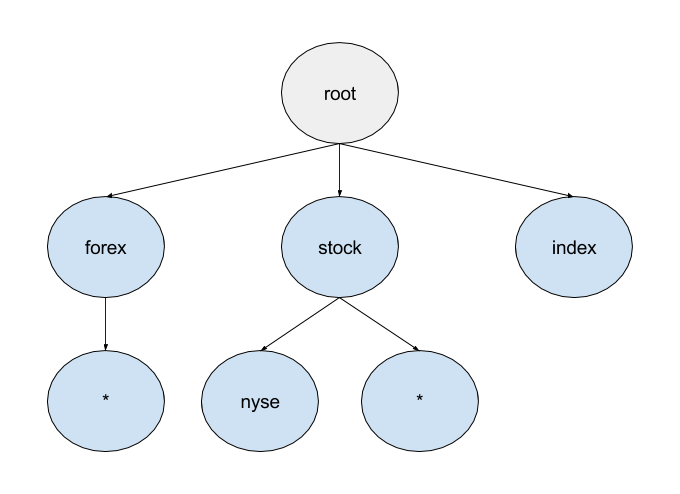
For the given set of subscriptions, the trie would look something like the following:

  • forex.*
  • stock.nyse
  • index
  • stock.*

You might be tempted to ask: “why do we even need the “*” nodes? When someone subscribes to stock.*, just follow all branches after “stock” and add the subscriber.” This would indeed move the backtracking cost from the read path to the write path, but—like the first inverted bitmap we looked at—it only works if the search space is known ahead of time. It would also largely negate the memory-usage benefits we’re looking for since it would require pre-indexing all topics while requiring a finite search space.

It turns out, this trie technique is how systems like ZeroMQ and RabbitMQ implement their topic matching due to its balance between space and time complexity and overall performance predictability.

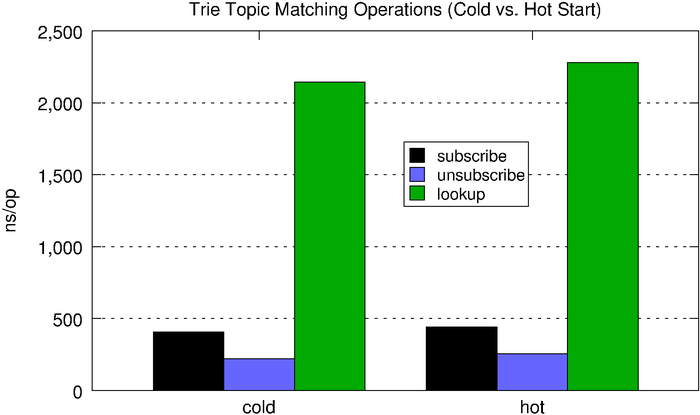
subscribe unsubscribe lookup
cold 406ns 221ns 2,145ns
hot 443ns 257ns 2,278ns

We can see that, compared to the optimized inverted bitmap, the trie performs much more predictably with relation to the number of subscriptions held.

Concurrent Subscription Trie

One thing we haven’t paid much attention to so far is concurrency. Indeed, message-oriented middleware is typically highly concurrent since they have to deal with heavy IO (reading messages from the wire, writing messages to the wire, reading messages from disk, writing messages to disk, etc.) and CPU operations (like topic matching and routing). Subscribe, unsubscribe, and lookups are usually all happening in different threads of execution. This is especially important when we want to talk advantage of multi-core processors.

It wasn’t shown, but all of the preceding algorithms used global locks to ensure thread safety between read and write operations, making the data structures safe for concurrent use. However, the microbenchmarks don’t really show the impact of this, which we will see momentarily.

Lock-freedom, which I’ve written about, allows us to increase throughput at the expense of increased tail latency.

Lock-free concurrency means that while a particular thread of execution may be blocked, all CPUs are able to continue processing other work. For example, imagine a program that protects access to some resource using a mutex. If a thread acquires this mutex and is subsequently preempted, no other thread can proceed until this thread is rescheduled by the OS. If the scheduler is adversarial, it may never resume execution of the thread, and the program would be effectively deadlocked. A key point, however, is that the mere lack of a lock does not guarantee a program is lock-free. In this context, “lock” really refers to deadlock, livelock, or the misdeeds of a malevolent scheduler.

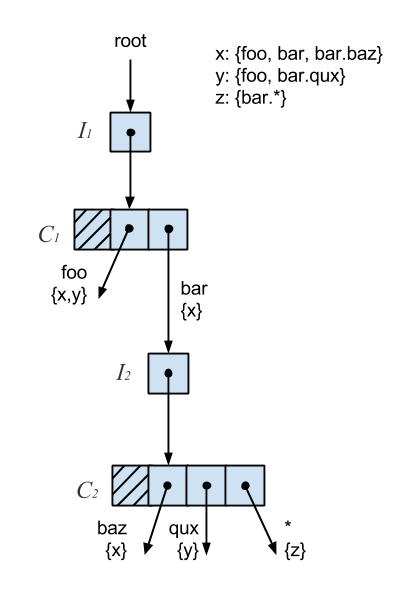
The concurrent subscription trie, or CS-trie,  is a new take on the trie-based solution described earlier. It combines the idea of the topic-matching trie with that of a Ctrie, or concurrent trie, which is a non-blocking concurrent hash trie.

The fundamental problem with the trie, as it relates to concurrency, is it requires a global lock, which severely limits throughput. To address this, the CS-trie uses indirection nodes, or I-nodes, which remain present in the trie even as the nodes above and below change. Subscriptions are then added or removed by creating a copy of the respective node, and performing a CAS on its parent I-node. This allows us to add, remove, and lookup subscriptions concurrently and in a lock-free, linearizable manner.

For the given set of subscribers, labeled x, y, and z, the CS-trie would look something like the following:

  • x = foo, bar, bar.baz
  • y = foo, bar.qux
  • z = bar.*

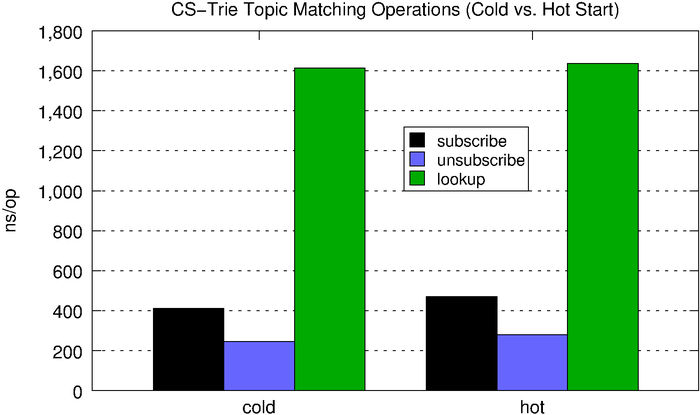
Lookups on the CS-trie perform, on average, better than the standard trie, and the CS-trie scales better with respect to concurrent operations.

subscribe unsubscribe lookup
cold 412ns 245ns 1,615ns
hot 471ns 280ns 1,637ns

Latency Comparison

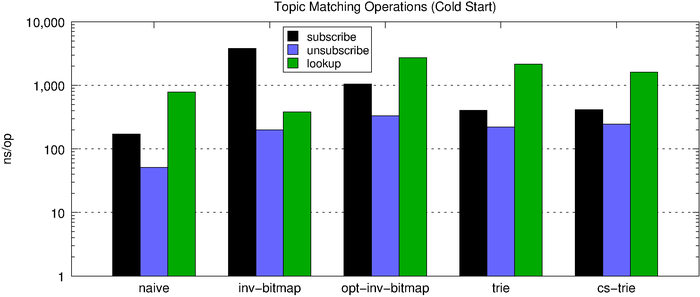
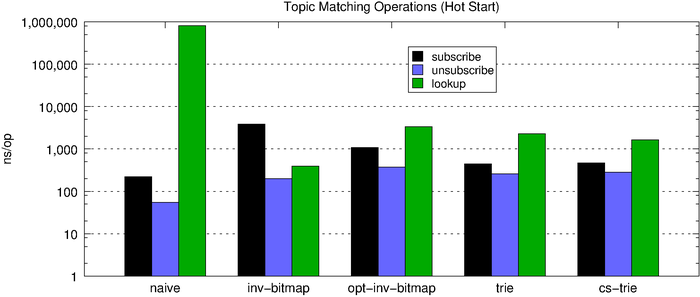
The chart below shows the topic-matching operation latencies for all of the algorithms side-by-side. First, we look at the performance of a cold start (no subscriptions) and then the performance of a hot start (1,000 subscriptions).

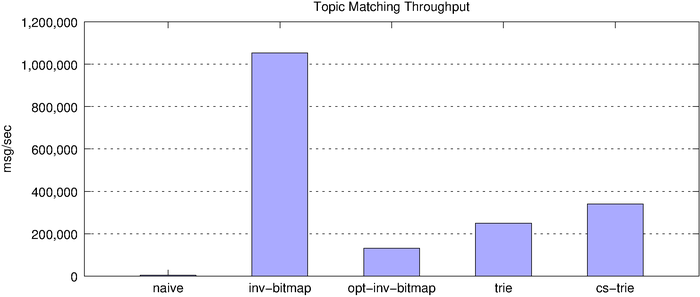
Throughput Comparison

So far, we’ve looked at the latency of individual topic-matching operations. Next, we look at overall throughput of each of the algorithms and their memory footprint.

 algorithm msg/sec
naive  4,053.48
inverted bitmap  1,052,315.02
optimized inverted bitmap  130,705.98
trie  248,762.10
cs-trie  340,910.64

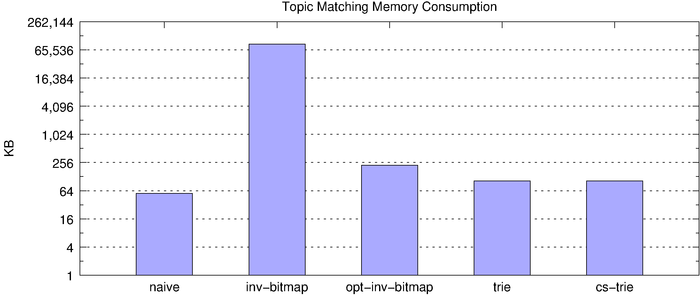
On the surface, the inverted bitmap looks like the clear winner, clocking in at over 1 million matches per second. However, we know the inverted bitmap does not scale and, indeed, this becomes clear when we look at memory consumption, underscored by the fact that the below chart uses a log scale.

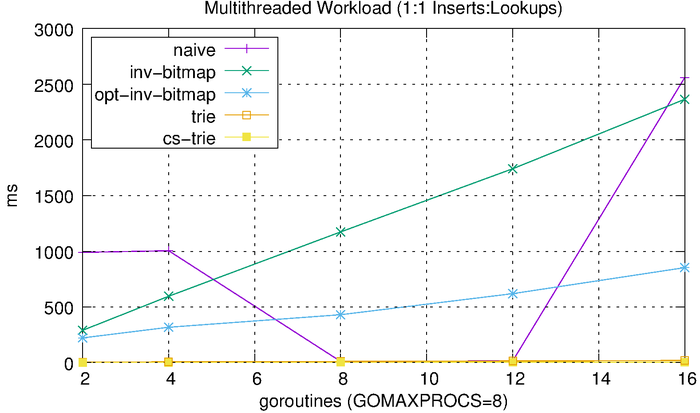
Scalability with Respect to Concurrency

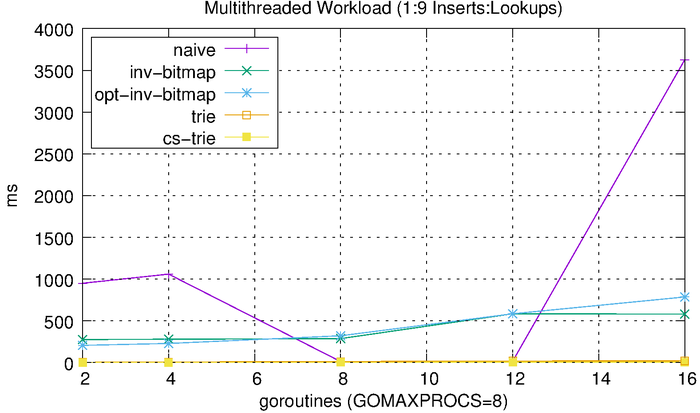
Lastly, we’ll look at how each of these algorithms scales with respect to concurrency. We do this by performing concurrent operations and varying the level of concurrency and number of operations. We start with a 50-50 split between reads and writes. We vary the number of goroutines from 2 to 16 (the benchmark was run using a 2.6 GHz Intel Core i7 processor with 8 logical cores). Each goroutine performs 1,000 reads or 1,000 writes. For example, the 2-goroutine benchmark performs 1,000 reads and 1,000 writes, the 4-goroutine benchmark performs 2,000 reads and 2,000 writes, etc. We then measure the total amount of time needed to complete the workload.

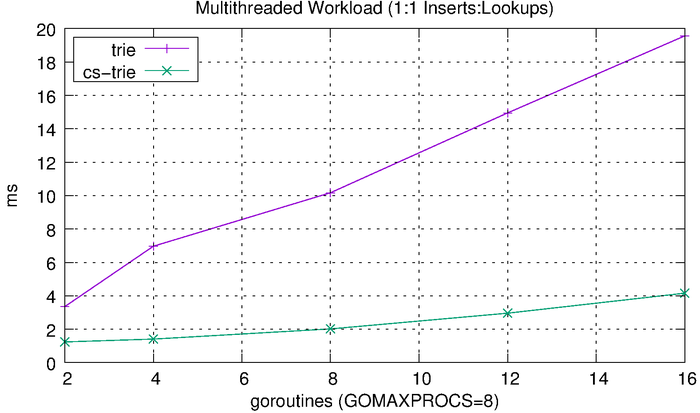
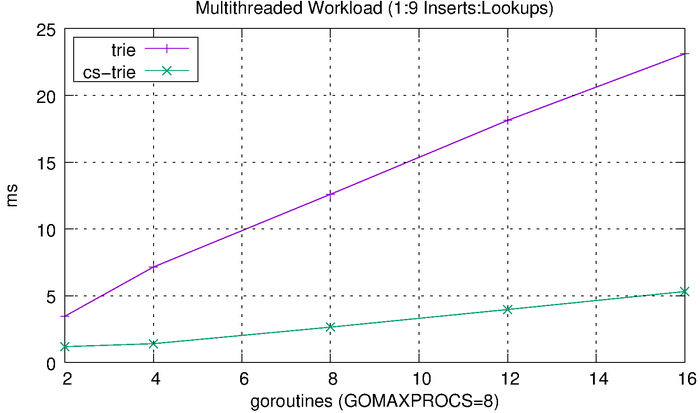
We can see that the tries hardly even register on the scale above, so we’ll plot them separately.

The tries are clearly much more efficient than the other solutions, but the CS-trie in particular scales well to the increased workload and concurrency.

Since most workloads are heavily biased towards reads over writes, we’ll run a separate benchmark that uses a 90-10 split reads and writes. This should hopefully provide a more realistic result.

The results look, more or less, like what we would expect, with the reduced writes improving the inverted bitmap performance. The CS-trie still scales quite well in comparison to the global-lock trie.

Conclusion

As we’ve seen, there are several approaches to consider to implement fast topic matching. There are also several aspects to look at: read/write access patterns, time complexity, space complexity, throughput, and latency.

The naive hashmap solution is generally a poor choice due to its prohibitively expensive lookup time. Inverted bitmaps offer a better solution. The standard implementation is reasonable if the search space is finite, small, and known a priori, especially if read latency is critical. The space-optimized version is a better choice for scalability, offering a good balance between read and write performance while keeping a small memory footprint. The trie is an even better choice, providing lower latency than the optimized inverted bitmap and consuming less memory. It’s particularly good if the subscription tree is sparse and topics are not known a priori. Lastly, the concurrent subscription trie is the best option if there is high concurrency and throughput matters. It offers similar performance to the trie but scales better. The only downside is an increase in implementation complexity.

Posted on

Stream Processing and Probabilistic Methods: Data at Scale

Stream processing and related abstractions have become all the rage following the rise of systems like Apache Kafka, Samza, and the Lambda architecture. Applying the idea of immutable, append-only event sourcing means we’re storing more data than ever before. However, as the cost of storage continues to decline, it’s becoming more feasible to store more data for longer periods of time. With immutability, how the data lives isn’t interesting anymore. It’s all about how it moves.

The shifting landscape of data architecture parallels the way we’re designing systems today. Specifically, the evolution of monolithic to service-oriented architecture necessitates a change in the way we do data integration. The traditional normalization approach doesn’t cut it. Our systems are composed of databases, caches, search indexes, data warehouses, and a multitude of other components. Moreover, there’s an increasing demand for online, real-time processing of this data that’s tantamount to the growing popularity of large-scale, offline processing along the lines of Hadoop. This presents an interesting set of new challenges, namely, how do we drink from the firehose without getting drenched?

The answer most likely lies in frameworks like Samza, Storm, and Spark Streaming. Similarly, tools like StatsD solve the problem of collecting real-time analytics. However, this discussion is meant to explore some of the primitives used in stream processing. The ideas extend far beyond event sourcing, generalizing to any type of data stream, unbounded or not.

Batch vs. Streaming

With offline or batch processing, we often have some heuristics which provide insight into our data set, and we can typically afford multiple passes of the data. Without a strict time constraint, data structures are less important. We can store the entire data set on disk (or perhaps across a distributed file system) and process it in batches.

With streaming data, however, there’s a need for near real-time processing—collecting analytics, monitoring and alerting, updating search indexes and caches, etc. With web crawlers, we process a stream of URLs and documents and produce indexed content. With websites, we process a stream of page views and update various counters and gauges. With email, we process a stream of text and produce a filtered, spam-free inbox. These cases involve massive, often limitless data sets. Processing that data online can’t be done with the conventional ETL or MapReduce-style methods, and unless you’re doing windowed processing, it’s entirely impractical to store that data in memory.

Framing the Problem

As a concrete example of stream processing, imagine we want to count the number of distinct document views across a large corpus, say, Wikipedia. A naive solution would be to use a hash table which maps a document to a count. Wikipedia has roughly 35 million pages. Let’s assume each document is identified by a 16-byte GUID, and the counters are stored as 8-byte integers. This means we need in the ball park of a gigabyte of memory. Given today’s hardware, this might not sound completely unreasonable, but now let’s say we want to track views per unique IP address. We see that this approach quickly becomes intractable.

To illustrate further, consider how to count the cardinality of IP addresses which access our website. Instead of a hash table, we can use a bitmap or sparse bit array to count addresses. There are over four billion possible distinct IPv4 addresses. Sure, we could allocate half a gigabyte of RAM, but if you’re developing performance-critical systems, large heap sizes are going to kill you, and this overhead doesn’t help. ((Granted, if you’re sensitive to garbage-collection pauses, you may be better off using something like C or Rust, but that’s not always the most practical option.))

A Probabilistic Approach

Instead, we turn to probabilistic ways of solving these problems. Probabilistic algorithms and data structures seem to be oft-overlooked, or maybe purposely ignored, by system designers despite the theory behind them having been around for a long time in many cases. The goal should be to move these from the world of academia to industry because they are immensely useful and widely neglected.

Probabilistic solutions trade space and performance for accuracy. While a loss in precision may be a cause for concern to some, the fact is with large data streams, we have to trade something off to get real-time insight. Much like the CAP theorem, we must choose between consistency (accuracy) and availability (online). With CAP, we can typically adjust the level in which that trade-off occurs. This space/performance-accuracy exchange behaves very much the same way.

The literature can get pretty dense, so let’s look at what some of these approaches are and the problems they solve in a way that’s (hopefully) understandable.

Bloom Filters

The Bloom filter is probably the most well-known and, conceptually, simplest probabilistic data structure. It also serves as a good foundation because there are a lot of twists you can put on it. The theory provides a kernel from which many other probabilistic solutions are derived, as we will see.

Bloom filters answer a simple question: is this element a member of a set? A normal set requires linear space because it stores every element. A Bloom filter doesn’t store the actual elements, it merely stores the “membership” of them. It uses sub-linear space opening the possibility for false positives, meaning there’s a non-zero probability it reports an item is in the set when it’s actually not. This has a wide range of applications. For example, a Bloom filter can be placed in front of a database. When a query for a piece of data comes in and the filter doesn’t contain it, we completely bypass the database.

The Bloom filter consists of a bit array of length m and k hash functions. Both of these parameters are configurable, but we can optimize them based on a desired rate of false positives. Each bit in the array is initially unset. When an element is “added” to the filter, it’s hashed by each of the k functions, h1…hk, and modded by m, resulting in k indices into the bit array. Each bit at the respective index is set.

To query the membership of an element, we hash it and check if each bit is set. If any of them are zero, we know the item isn’t in the set. What happens when two different elements hash to the same index? This is where false positives are introduced. If the bits aren’t set, we know the element wasn’t added, but if they are, it’s possible that some other element or group of elements hashed to the same indices. Bloom filters have false positives, but false negatives are impossible—a member will never be reported incorrectly as a non-member. Unfortunately, this also means items can’t be removed from the filter.

It’s clear that the likelihood of false positives increases with each element added to the filter. We can target a specific probability of false positives by selecting an optimal value for m and k for up to n insertions. ((The math behind determining optimal m and k is left as an exercise for the reader.)) While this implementation works well in practice, it has a drawback in that some elements are potentially more sensitive to false positives than others. We can solve this problem by partitioning the m bits among the k hash functions such that each one produces an index over its respective partition. As a result, each element is always described by exactly k bits. This prevents any one element from being especially sensitive to false positives. Since calculating k hashes for every element is computationally expensive, we can actually perform a single hash and derive k hashes from it for a significant speedup. ((Less Hashing, Same Performance: Building a Better Bloom Filter discusses the use of two hash functions to simulate additional hashes. We can use a 64-bit hash, such as FNV, and use the upper and lower 32-bits as two different hashes.))

A Bloom filter eventually reaches a point where all bits are set, which means every query will indicate membership, effectively making the probability of false positives one. The problem with this is it requires a priori knowledge of the data set in order to select optimal parameters and avoid “overfilling.” Consequently, Bloom filters are ideal for offline processing and not so great for dealing with streams. Next, we’ll look at some variations of the Bloom filter which attempt to deal with this issue.

Scalable Bloom Filter

As we saw earlier, traditional Bloom filters are a great way to deal with set-membership problems in a space-efficient way, but they require knowing the size of the data set ahead of time in order to be effective. The Scalable Bloom Filter (SBF) was introduced by Almeida et al. as a way to cope with the capacity dilemma.

The Scalable Bloom Filter dynamically adapts to the size of the data set while enforcing a tight upper bound on the rate of false positives. Like the classic Bloom filter, false negatives are impossible. The SBF is essentially an array of Bloom filters with geometrically decreasing false-positive rates. New elements are added to the last filter. When this filter becomes “full”—more specifically, when it reaches a target fill ratio—a new filter is added with a tightened error probability. A tightening ratio, r, controls the growth of new filters.

Testing membership of an element consists of checking each of the filters. The geometrically decreasing false-positive rate of each filter is an interesting property. Since the fill ratio determines when a new filter is added, it turns out this progression can be modeled as a Taylor series which allows us to provide a tight upper bound on false positives using an optimal fill ratio of 0.5 (once the filter is 50% full, a new one is added). The compounded probability over the whole series converges to a target value, even accounting for an infinite series.

We can limit the error rate, but obviously the trade-off is that we end up allocating memory proportional to the size of the data set since we’re continuously adding filters. We also pay some computational cost on adds. Amortized, the cost of filter insertions is negligible, but for every add we must compute the current fill ratio of the filter to determine if a new filter needs to be added. Fortunately, we can optimize this by computing an estimated fill ratio. If we keep a running count of the items added to the filter, n, the approximate current fill ratio, p, can be obtained from the Taylor series expansion with p \approx 1-e^{-n/m} where m is the number of bits in the filter. Calculating this estimate turns out to be quite a bit faster than computing the actual fill ratio—fewer memory reads.

To provide some context around performance, adds in my Go implementation of a classic Bloom filter take about 166 ns on my MacBook Pro, and membership tests take 118 ns. With the SBF, adds take 422 ns and tests 113 ns. This isn’t a completely fair comparison since, as the SBF grows over time, tests require scanning through each filter, but certainly the add numbers are intuitive.

Scalable Bloom Filters are useful for cases where the size of the data set isn’t known a priori and memory constraints aren’t of particular concern. It’s an effective variation of a regular Bloom filter which generally requires space allocation orders-of-magnitude larger than the data set to allow enough headroom.

Stable Bloom Filter

Classic Bloom filters aren’t great for streaming data, and Scalable Bloom Filters, while a better option, still present a memory problem. Another derivative, the Stable Bloom Filter (SBF), was proposed by Deng and Rafiei as a technique for detecting duplicates in unbounded data streams with limited space. Most solutions work by dividing the stream into fixed-size windows and solving the problem within that discrete space. This allows the use of traditional methods like the Bloom filter.

The SBF attempts to approximate duplicates without the use of windows. Clearly, we can’t store the entire history of an infinite stream in limited memory. Instead, the thinking is more recent data has more value than stale data in many scenarios. As an example, web crawlers may not care about redundantly fetching a web page that was crawled a long time ago compared to fetching a page that was crawled more recently. With this impetus, the SBF works by representing more recent data while discarding old information.

The Stable Bloom Filter tweaks the classic Bloom filter by replacing the bit array with an array of m cells, each allocated d bits. The cells are simply counters, initially set to zero. The maximum value, Max, of a cell is 2^d-1. When an element is added, we first have to ensure space for it. This is done by selecting P random cells and decrementing their counters by one, clamping to zero. Next, we hash the element to k cells and set their counters to Max. Testing membership consists of probing the k cells. If any of them are zero, it’s not a member. The Bloom filter is actually a special case of an SBF where d is one and P is zero.

Like traditional Bloom filters, an SBF has a non-zero probability of false positives, which is controlled by several parameters. Unlike the Bloom filter, an SBF has a tight upper bound on the rate of false positives while introducing a non-zero rate of false negatives. The false-positive rate of a classic Bloom filter eventually reaches one, after which all queries result in a false positive. The stable-point property of an SBF means the false-positive rate asymptotically approaches a configurable fixed constant.

Stable Bloom Filters lend themselves to situations where the size of the data set isn’t known ahead of time and memory is bounded. For example, an SBF can be used to deduplicate events from an unbounded event stream with a specified upper bound on false positives and minimal false negatives. In particular, if the stream is not uniformly distributed, meaning duplicates are likely to be grouped closer together, the rate of false positives becomes immaterial.

Counting Bloom Filter

Conventional Bloom filters don’t allow items to be removed. The Stable Bloom Filter, on the other hand, works by evicting old data, but its API doesn’t expose a way to remove specific elements. The Counting Bloom Filter (CBF) is yet another twist on this structure. Introduced by Fan et al. in Summary Cache: A Scalable Wide-Area Web Cache Sharing Protocol, the CBF provides a way of deleting data from a filter.

It’s actually a very straightforward approach. The filter comprises an array of n-bit buckets similar to the Stable Bloom Filter. When an item is added, the corresponding counters are incremented, and when it’s removed, the counters are decremented.

Obviously, a CBF takes n-times more space than a regular Bloom filter, but it also has a scalability limit. Unless items are removed frequently enough, a counting filter’s false-positive probability will approach one. We need to dimension it accordingly, and this normally requires inferring from our data set. Likewise, since the CBF allows removals, it exposes an opportunity for false negatives. The multi-bit counters diminish the rate, but it’s important to be cognizant of this property so the CBF can be applied appropriately.

Inverse Bloom Filter

One of the distinguishing features of Bloom filters is the guarantee of no false negatives. This can be a valuable invariant, but what if we want the opposite of that? Is there an efficient data structure that can offer us no false positives with the possibility of false negatives? The answer is deceptively simple.

Jeff Hodges describes a rather trivial—yet strikingly pragmatic—approach which he calls the “opposite of a Bloom filter.” Since that name is a bit of a mouthful, I’m referring to this as the Inverse Bloom Filter (IBF).

The Inverse Bloom Filter may report a false negative but can never report a false positive. That is, it may indicate that an item has not been seen when it actually has, but it will never report an item as seen which it hasn’t come across. The IBF behaves in a similar manner to a fixed-size hash map of m buckets which doesn’t handle conflicts, but it provides lock-free concurrency using an underlying CAS.

The test-and-add operation hashes an element to an index in the filter. We take the value at that index while atomically storing the new value, then the old value is compared to the new one. If they differ, the new value wasn’t a member. If the values are equivalent, it was in the set.

The Inverse Bloom Filter is a nice option for dealing with unbounded streams or large data sets due to its limited memory usage. If duplicates are close together, the rate of false negatives becomes vanishingly small with an adequately sized filter.

HyperLogLog

Let’s revisit the problem of counting distinct IP addresses visiting a website. One solution might be to allocate a sparse bit array proportional to the number of IPv4 addresses. Alternatively, we could combine a Bloom filter with a counter. When an address comes in and it’s not in the filter, increment the count. While these both work, they’re not likely to scale very well. Rather, we can apply a probabilistic data structure known as the HyperLogLog (HLL). First presented by Flajolet et al. in 2007, HyperLogLog is an algorithm which approximately counts the number of distinct elements, or cardinality, of a multiset (a set which allows multiple occurrences of its elements).

Imagine our stream as a series of coin tosses. Someone tells you the most heads they flipped in a row was three. You can guess that they didn’t flip the coin very many times. However, if they flipped 20 heads in a row, it probably took them quite a while. This seems like a really unconvincing way of estimating the number of tosses, but from this kernel of thought grows a fruitful idea.

HLL replaces heads and tails with zeros and ones. Instead of counting the longest run of heads, it counts the longest run of leading zeros in a binary hash. Using a good hash function means that the values are, more or less, statistically independent and uniformly distributed. If the maximum run of leading zeros is n, the number of distinct elements in the set is approximately 2^n. But wait, what’s the math behind this? If we think about it, half of all binary numbers start with 1. Each additional bit divides the probability of a run further in half; that is, 25% start with 01, 12.5% start with 001, 6.25% start with 0001, ad infinitum. Thus, the probability of a run of length n is 2^{-(n+1)}.

Like flipping a coin, there’s potential for an enormous amount of variance with this technique. For instance, it’s entirely possible—though unlikely—that you flip 20 heads in a row on your first try. One experiment doesn’t provide enough data, so instead you flip 10 coins. HyperLogLog uses a similar strategy to reduce variance by splitting the stream up across a set of buckets, or registers, and applying the counting algorithm on the values in each one. It tracks the longest run of zeros in every register, and the total cardinality is computed by taking the harmonic mean across all registers. The harmonic mean is used to discount outliers since the distribution of values tends to skew towards the right. We can increase accuracy by adding more registers, which of course comes at the expense of performance and memory.

HyperLogLog is a remarkable algorithm. It almost feels like magic, and it’s exceptionally useful for working with data streams. HLL has a fraction of the memory footprint of other solutions. In fact, it’s usually several orders of magnitude while remaining surprisingly accurate.

Count-Min Sketch

HyperLogLog is a great option to efficiently count the number of distinct elements in a stream using a minimal amount of space, but it only gives us cardinality. What about counting the frequencies of specific elements? Cormode and Muthukrishnan developed the Count-Min sketch (CM sketch) to approximate the occurrences of different event types from a stream of events.

In contrast to a hash table, the Count-Min sketch uses sub-linear space to count frequencies. It consists of a matrix with w columns and d rows. These parameters determine the trade-off between space/time constraints and accuracy. Each row has an associated hash function. When an element arrives, it’s hashed for each row. The corresponding index in the rows are incremented by one. In this regard, the CM sketch shares some similarities with the Bloom filter.

count_min_sketch

The frequency of an element is estimated by taking the minimum of all the element’s respective counter values. The thought process here is that there is possibility for collisions between elements, which affects the counters for multiple items.  Taking the minimum count results in a closer approximation.

The Count-Min sketch is an excellent tool for counting problems for the same reasons as HyperLogLog. It has a lot of similarities to Bloom filters, but where Bloom filters effectively represent sets, the CM sketch considers multisets.

MinHash

The last probabilistic technique we’ll briefly look at is MinHash. This algorithm, invented by Andrei Broder, is used to quickly estimate the similarity between two sets. This has a variety of uses, such as detecting duplicate bodies of text and clustering or comparing documents.

MinHash works, in part, by using the Jaccard coefficient, a statistic which represents the size of the intersection of two sets divided by the size of the union:

J(A,B) = {{|A \cap B|}\over{|A \cup B|}}

This provides a measure of how similar the two sets are, but computing the intersection and union is expensive. Instead, MinHash essentially works by comparing randomly selected subsets through element hashing. It resembles locality-sensitive hashing (LSH), which means that similar items have a greater tendency to map to the same hash values. This varies from most hashing schemes, which attempt to avoid collisions. Instead, LSH is designed to maximize collisions of similar elements.

MinHash is one of the more difficult algorithms to fully grasp, and I can’t even begin to provide a proper explanation. If you’re interested in how it works, read the literature but know that there are a number of variations of it. The important thing is to know it exists and what problems it can be applied to.

In Practice

We’ve gone over several fundamental primitives for processing large data sets and streams while solving a few different types of problems. Bloom filters can be used to reduce disk reads and other expensive operations. They can also be purposed to detect duplicate events in a stream or prune a large decision tree. HyperLogLog excels at counting the number of distinct items in a stream while using minimal space, and the Count-Min sketch tracks the frequency of particular elements. Lastly, the MinHash method provides an efficient mechanism for comparing the similarity between documents. This has a number of applications, namely around identifying duplicates and characterizing content.

While there are no doubt countless implementations for most of these data structures and algorithms, I’ve been putting together a Go library geared towards providing efficient techniques for stream processing called Boom Filters. It includes implementations for all of the probabilistic data structures outlined above. As streaming data and real-time consumption grow more and more prominent, it will become important that we have the tools and understanding to deal with them. If nothing else, it’s valuable to be aware of probabilistic methods because they often provide accurate results at a fraction of the cost. These things aren’t just academic research, they form the basis for building online, high-performance systems at scale.

Posted on

Not Invented Here

Engineers love engineering things. The reason is self-evident (and maybe self-fulfilling—why else would you be an engineer?). We like to think we’re pretty good at solving problems. Unfortunately, this mindset can, on occasion, yield undesirable consequences which might not be immediately apparent but all the while damaging.

Developers are all in tune with the idea of “don’t reinvent the wheel,” but it seems to be eschewed sometimes, deliberately or otherwise. People don’t generally write their own merge sort, so why would they write their own consensus protocol? Anecdotally speaking, they do.

Not-Invented-Here Syndrome is a very real thing. In many cases, consciously or not, it’s a cultural problem. In others, it’s an engineering one. Camille Fournier’s blog post on ZooKeeper helps to illustrate this point and provide some context. In it, she describes why some distributed systems choose to rely on external services, such as ZooKeeper, for distributed coordination, while others build in their own coordination logic.

We draw a parallel between distributed systems and traditional RDBMSs, which typically implement their own file system and other low-level facilities. Why? Because it’s their competitive advantage. SQL databases sell because they offer finely tuned performance, and in order to do that, they need to control these things that the OS otherwise provides. Distributed databases like Riak sell because they own the coordination logic, which helps promote their competitive advantage. This follows what Joel Spolsky says about NIH Syndrome in that “if it’s a core business function—do it yourself, no matter what.”

If you’re developing a computer game where the plot is your competitive advantage, it’s OK to use a third party 3D library. But if cool 3D effects are going to be your distinguishing feature, you had better roll your own.

This makes a lot of sense. My sorting algorithm is unlikely to provide me with a competitive edge, but something else might, even if it’s not particularly novel.

So in some situations, homegrown is justifiable, but that’s not always the case. Redis’ competitive advantage is its predictably low latencies and data structures. Does it make sense for it to implement its own clustering and leader election protocols? Maybe, but this is where NIH can bite you. If what you’re doing is important and there’s precedent, lean on existing research and solutions. Most would argue write safety is important, and there is certainly precedent for leader election. Why not leverage that work? Things like Raft, Paxos, and Zab provide solutions which are proven using formal methods and are peer reviewed. That doesn’t mean new solutions can’t be developed, but they generally require model checking and further scrutiny to ensure correctness. Otherwise, you’ll inevitably run into problems. Implementing our own solutions can provide valuable insight, but leave them at home if they’re not rigorously approached. Rolling your own and calling it “good enough” is dishonest to your users if it’s not properly communicated.

Elasticsearch is another interesting case to look at. You might say Elasticsearch’s competitive advantage is its full-text search engine, but it’s not. Like Solr, it’s built on Lucene. Elasticsearch was designed from the ground-up to be distributed. This is what gives it a leg up over Solr and other similar search servers where horizontal scaling and fault tolerance were essentially tacked on. In a way, this resembles what happened with Redis, where failover and clustering were introduced as an afterthought. However, unlike Redis, which chose to implement its own failover coordination and cluster-membership protocol, Solr opted to use ZooKeeper as an external coordinator.

We see that Elasticsearch’s core advantage is its distributed nature. Following that notion, it makes sense for it to own that coordination, which is why its designers chose to implement their own internal cluster membership, ZenDisco. But it turns out writing cluster-membership protocols is really fucking hard, and unless you’ve written proofs for it, you probably shouldn’t do it at all. The analogy here would be writing your own encryption algorithm—there’s tons of institutional knowledge which has laid the groundwork for solutions which are well-researched and well-understood. That knowledge should be embraced in situations like this.

I don’t mean to pick on Redis and Elasticsearch. They’re both excellent systems, but they serve as good examples for this discussion. The problem is that users of these systems tend to overlook the issues exposed by this mentality. Frankly, few people would know problems exist unless they are clearly documented by vendors (and not sales people) and even then, how many people actually read the docs cover-to-cover? It’s essential we know a system’s shortcomings and edge cases so we can recognize which situations to apply it and, more important, which we should not.

You don’t have to rely on an existing third-party library or service. Believe it or not, this isn’t a sales pitch for ZooKeeper. If it’s a core business function, it probably makes sense to build it yourself as Joel describes. What doesn’t make sense, however, is to build out whatever that is without being cognizant of conventional wisdom. I’m amazed at how often people are willing to throw away institutional knowledge, either because they don’t seek it out or they think they can do better (without formal verification). If I have seen further, it is by standing on the shoulders of giants.

Posted on

Probabilistic Primality Testing

An exceedingly common question asked in coding interviews is to write a function, method, algorithm, whatever to determine if a number is prime. Prime numbers have a wide range of applications in computer science, particularly with regard to cryptography. The idea is that factoring large numbers into their prime factors is extremely difficult.

“Because both the system’s privacy and the security of digital money depend on encryption, a breakthrough in mathematics or computer science that defeats the cryptographic system could be a disaster. The obvious mathematical breakthrough would be the development of an easy way to factor large prime numbers.” -Bill Gates, The Road Ahead

Granted, for most programming positions, this question is asked not to test the candidate’s knowledge of determining primality, but rather as an exercise to gain insight into his or her thought process on a well-understood problem.

The Naive Approach

The common approach to this problem is a simple brute-force solution. That is, divide the number {n} by every integer from 2 to n-1 and check the remainder. This is certainly the easiest way to solve the problem.

This is also incredibly inefficient. We can improve it a bit by checking factors from 2 to n/2, but that still isn’t very good for huge numbers. If n is composite (i.e. it’s not prime), then it can be factored into two numbers, one of which must be less than or equal to \sqrt{n}. With this in mind, we can improve our algorithm even further.

These are the solutions your interviewer will probably be looking for, starting with the most naive approach and improving from that, but even the revised version is not very efficient.

Probabilistic Testing

A slightly more sophisticated way to go about checking primality is to use probabilistic testing. Probabilistic tests use numbers, a, chosen at random from some sample space. This technique introduces a probability of error which can be reduced by repeating the test with independently selected a values.

There are a number of different probabilistic primality tests, some better than others.  One of the more simple probabilistic primality tests is the Fermat primality test, which is based on Fermat’s little theorem and is used in PGP and RSA encryption. The theorem states that, if p is prime, then a^{p-1} \equiv 1 \pmod{p} where 1\leq a < p.

This method will indicate if p is a probable prime, but since we’re only selecting a single a value, the possibility of p being incorrectly identified as a prime is high. In such situations, a is referred to as a Fermat liar. As suggested earlier, we can minimize this probability by repeating the process k times and selecting k witnesses.

This allows us to improve the probability of correctly determining the primality of p by performing k iterations, in which the probability of error becomes vanishingly small for large values of k. Nonetheless, being probabilistic in nature, this algorithm is inherently nondeterministic, which is really just a fancy way of saying we can get different results on different runs for the same input.

Polynomial, Deterministic Algorithms

Only within the last decade has a deterministic, polynomial-time algorithm for testing primality been developed. In 2002, the AKS primality test was discovered, moving primality into the P complexity class. The algorithm determines if a given number is prime or composite in polynomial time, and it’s the first to be simultaneously general, polynomial, unconditional, and deterministic. Try busting that out at an interview.

For the mathematically inclined (of which I do not consider myself), primality presents some interesting uses and even more interesting problems. It’s remarkable that a fast, deterministic solution for such a well-defined problem was found only in the last 10 years, and it makes you wonder what tough problems will be solved in the next 10 years and beyond.