coordinated omission – Brave New Geek

February 13, 2016December 20, 2016

Benchmarking Message Queue Latency

About a year and a half ago, I published Dissecting Message Queues, which broke down a few different messaging systems and did some performance benchmarking. It was a naive attempt and had a lot of problems, but it was also my first time doing any kind of system benchmarking. It turns out benchmarking systems correctly is actually pretty difficult and many folks get it wrong. I don’t claim to have gotten it right, but over the past year and a half I’ve learned a lot, tried to build some better tools, and improve my methodology.

Tooling and Methodology

The Dissecting Message Queues benchmarks used a framework I wrote which published a specified number of messages effectively as fast as possible, received them, and recorded the end-to-end latency. There are several problems with this. First, load generation and consumption run on the same machine. Second, the system under test runs on the same machine as the benchmark client—both of these confound measurements. Third, running “pedal to the metal” and looking at the resulting latency isn’t a very useful benchmark because it’s not representative of a production environment (as Gil Tene likes to say, this is like driving your car as fast as possible, crashing it into a pole, and looking at the shape of the bumper afterwards—it’s always going to look bad). Lastly, the benchmark recorded average latency, which, for all intents and purposes, is a useless metric to look at.

I wrote Flotilla to automate “scaled-up” benchmarking—running the broker and benchmark clients on separate, distributed VMs. Flotilla also attempted to capture a better view of latency by looking at the latency distribution, though it only went up to the 99th percentile, which can sweep a lot of really bad things under the rug as we’ll see later. However, it still ran tests at full throttle, which isn’t great.

Bench is an attempt to get back to basics. It’s a simple, generic benchmarking library for measuring latency. It provides a straightforward Requester interface which can be implemented for various systems under test. Bench works by attempting to issue a fixed rate of requests per second and measuring the latency of each request issued synchronously. Latencies are captured using HDR Histogram, which observes the complete latency distribution and allows us to look, for example, at “six nines” latency.

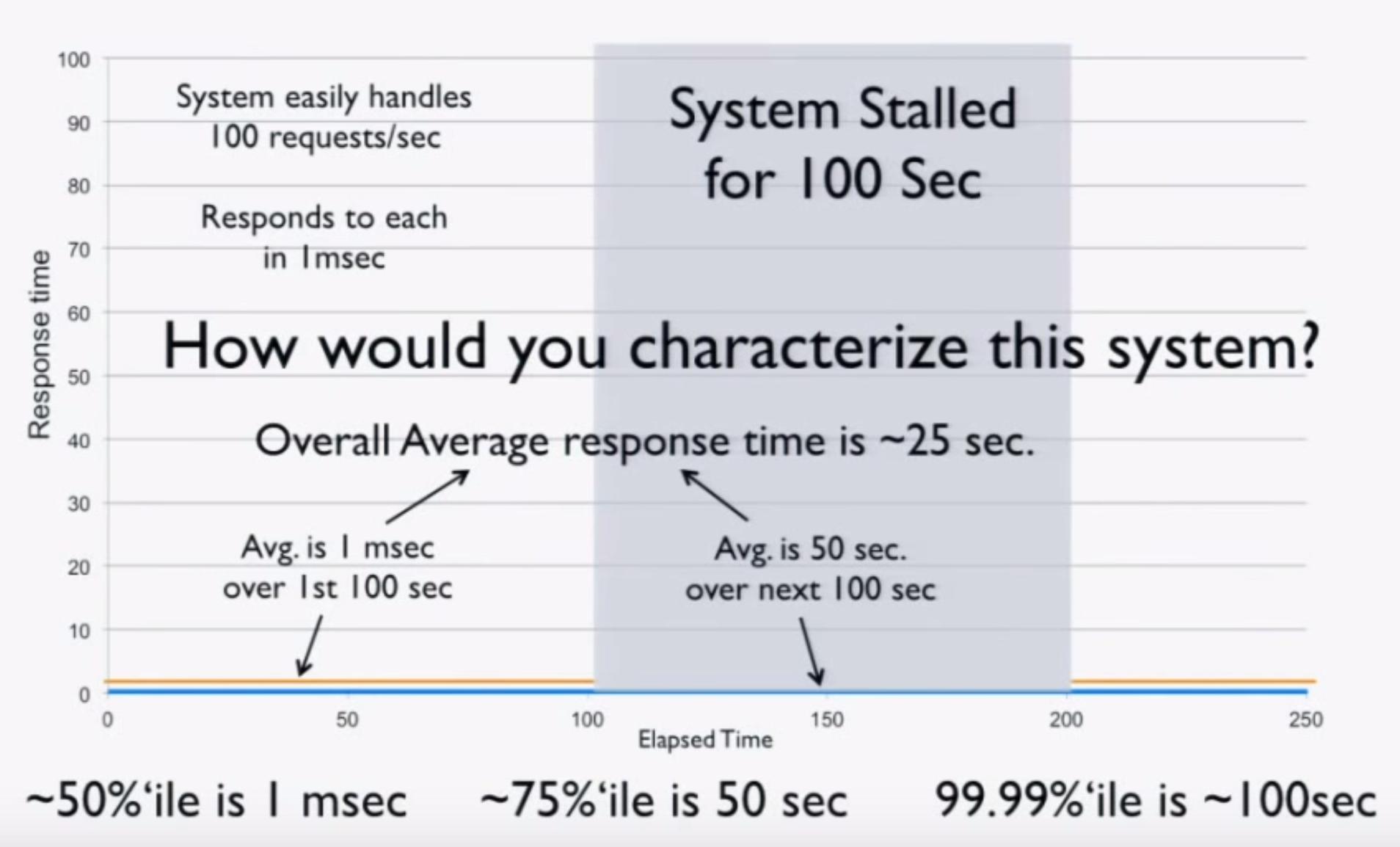
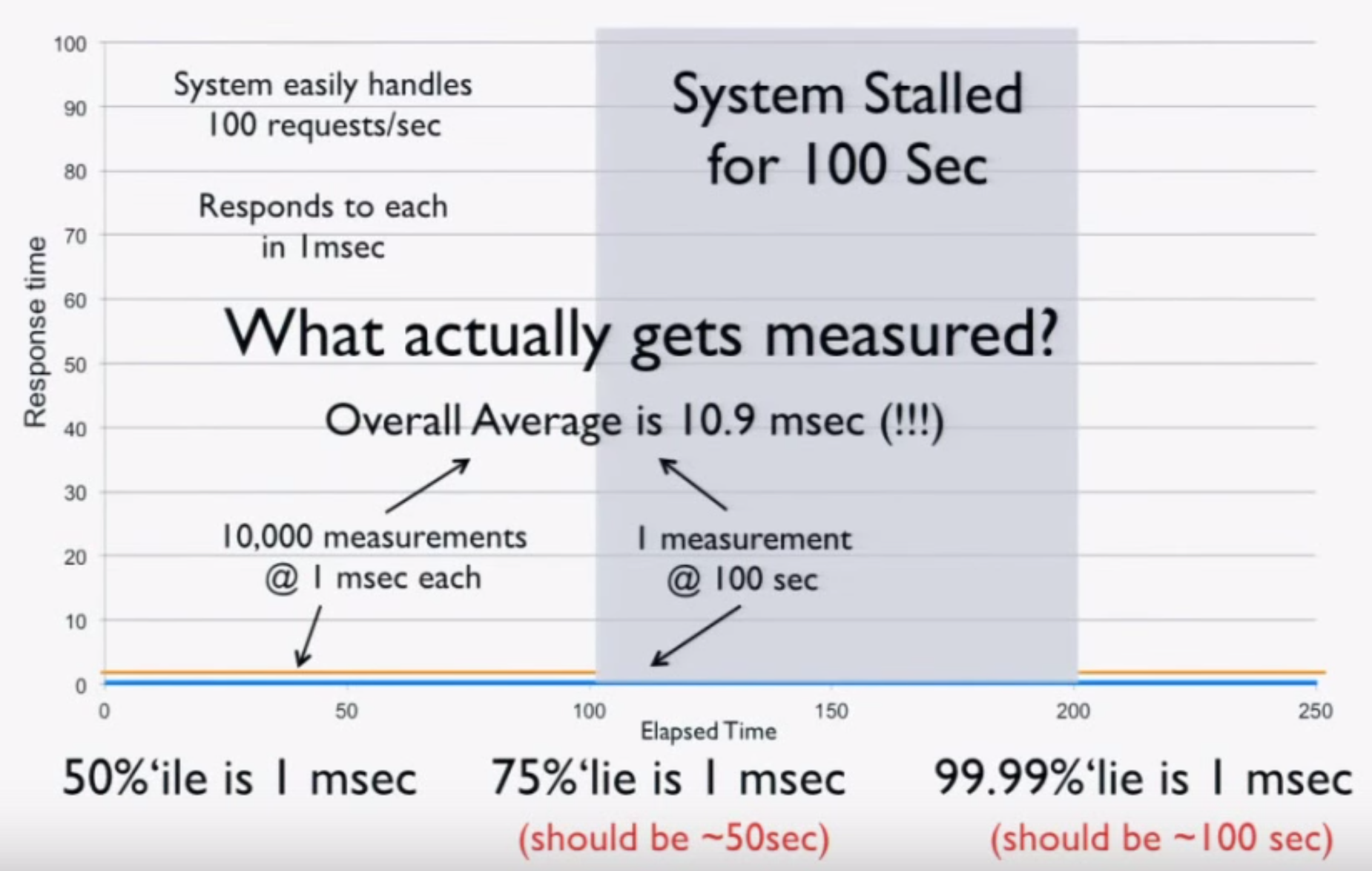
Introducing a request schedule allows us to measure latency for different configurations of request rate and message size, but in a “closed-loop” test, it creates another problem called coordinated omission. The problem with a lot of benchmarks is that they end up measuring service time rather than response time, but the latter is likely what you care about because it’s what your users experience.

The best way to describe service time vs. response time is to think of a cash register. The cashier might be able to ring up a customer in under 30 seconds 99% of the time, but 1% of the time it takes three minutes. The time it takes to ring up a customer is the service time, while the response time consists of the service time plus the time the customer waited in line. Thus, the response time is dependent upon the variation in both service time and the rate of arrival. When we measure latency, we really want to measure response time.

Now, let’s think about how most latency benchmarks work. They usually do this:

Note timestamp before request, t₀.
Make synchronous request.
Note timestamp after request, t₁.
Record latency t₁ – t₀.
Repeat as needed for request schedule.

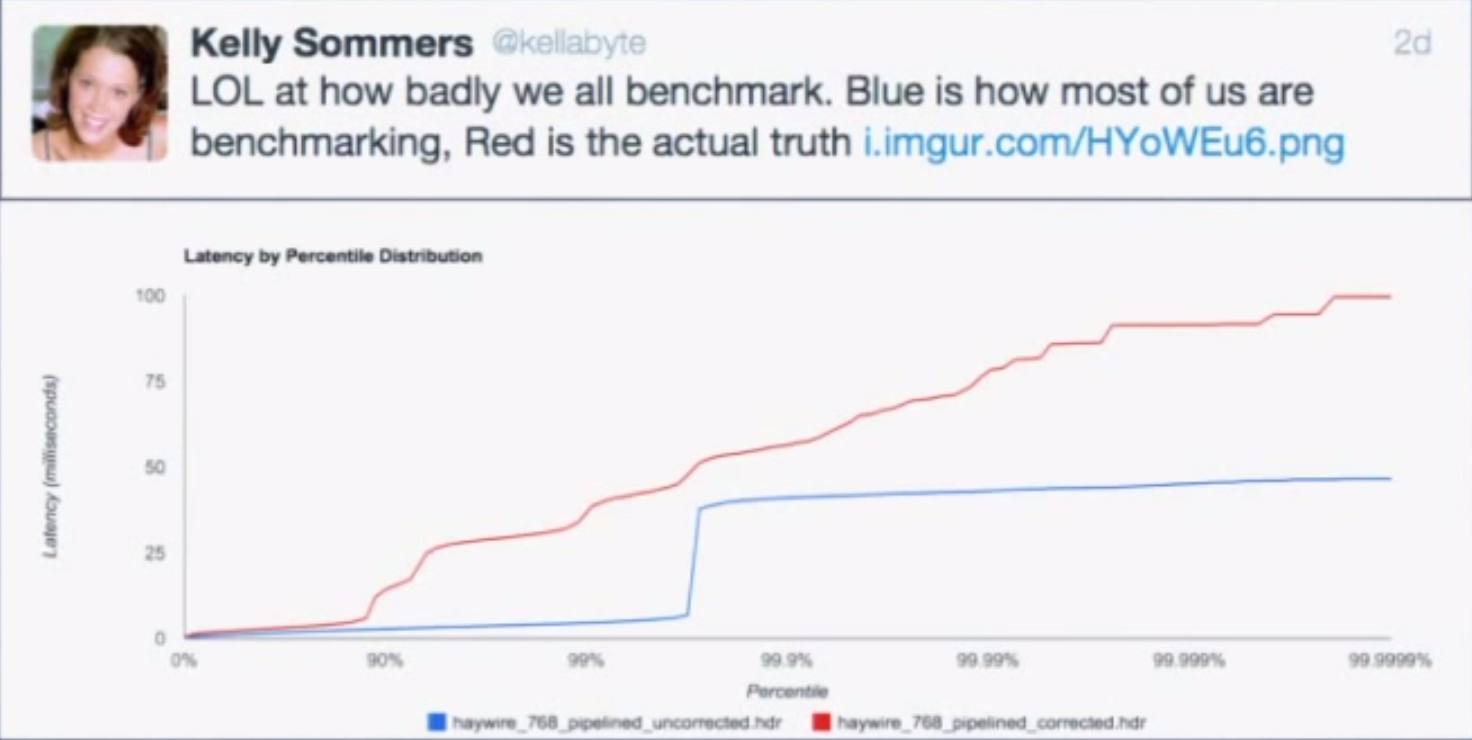
What’s the problem with this? Nothing, as long as our requests fit within the specified request schedule. For example, if we’re issuing 100 requests per second and each request takes 10 ms to complete, we’re good. However, if one request takes 100 ms to complete, that means we issued only one request during those 100 ms when, according to our schedule, we should have issued 10 requests in that window. Nine other requests should have been issued, but the benchmark effectively coordinated with the system under test by backing off. In reality, those nine requests waited in line—one for 100 ms, one for 90 ms, one for 80 ms, etc. Most benchmarks don’t capture this time spent waiting in line, yet it can have a dramatic effect on the results. The graph below shows the same benchmark with coordinated omission both uncorrected (red) and corrected (blue):

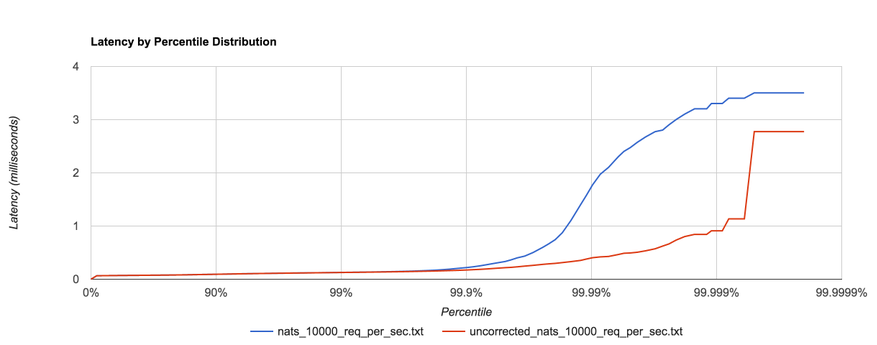
HDR Histogram attempts to correct coordinated omission by filling in additional samples when a request falls outside of its expected interval. We can also deal with coordinated omission by simply avoiding it altogether—always issue requests according to the schedule.

Message Queue Benchmarks

I benchmarked several messaging systems using bench—RabbitMQ (3.6.0), Kafka (0.8.2.2 and 0.9.0.0), Redis (2.8.4) pub/sub, and NATS (0.7.3). In this context, a “request” consists of publishing a message to the server and waiting for a response (i.e. a roundtrip). We attempt to issue requests at a fixed rate and correct for coordinated omission, then plot the complete latency distribution all the way up to the 99.9999th percentile. We repeat this for several configurations of request rate and request size. It’s also important to note that each message going to and coming back from the server are of the specified size, i.e. the “response” is the same size as the “request.”

The configurations used are listed below. Each configuration is run for a sustained 30 seconds.

256B requests at 3,000 requests/sec (768 KB/s)
1KB requests at 3,000 requests/sec (3 MB/s)
5KB requests at 2,000 requests/sec (10 MB/s)
1KB requests at 20,000 requests/sec (20.48 MB/s)
1MB requests at 100 requests/sec (100 MB/s)

These message sizes are mostly arbitrary, and there might be a better way to go about this. Though I think it’s worth pointing out that the Ethernet MTU is 1500 bytes, so accounting for headers, the maximum amount of data you’ll get in a single TCP packet will likely be between 1400 and 1500 bytes.

The system under test and benchmarking client are on two different m4.xlarge EC2 instances (2.4 GHz Intel Xeon Haswell, 16GB RAM) with enhanced networking enabled.

Redis and NATS

Redis pub/sub and NATS have similar performance characteristics. Both offer very lightweight, non-transactional messaging with no persistence options (discounting Redis’ RDB and AOF persistence, which don’t apply to pub/sub), and both support some level of topic pattern matching. I’m hesitant to call either a “message queue” in the traditional sense, so I usually just refer to them as message brokers or buses. Because of their ephemeral nature, both are a nice choice for low-latency, lossy messaging.

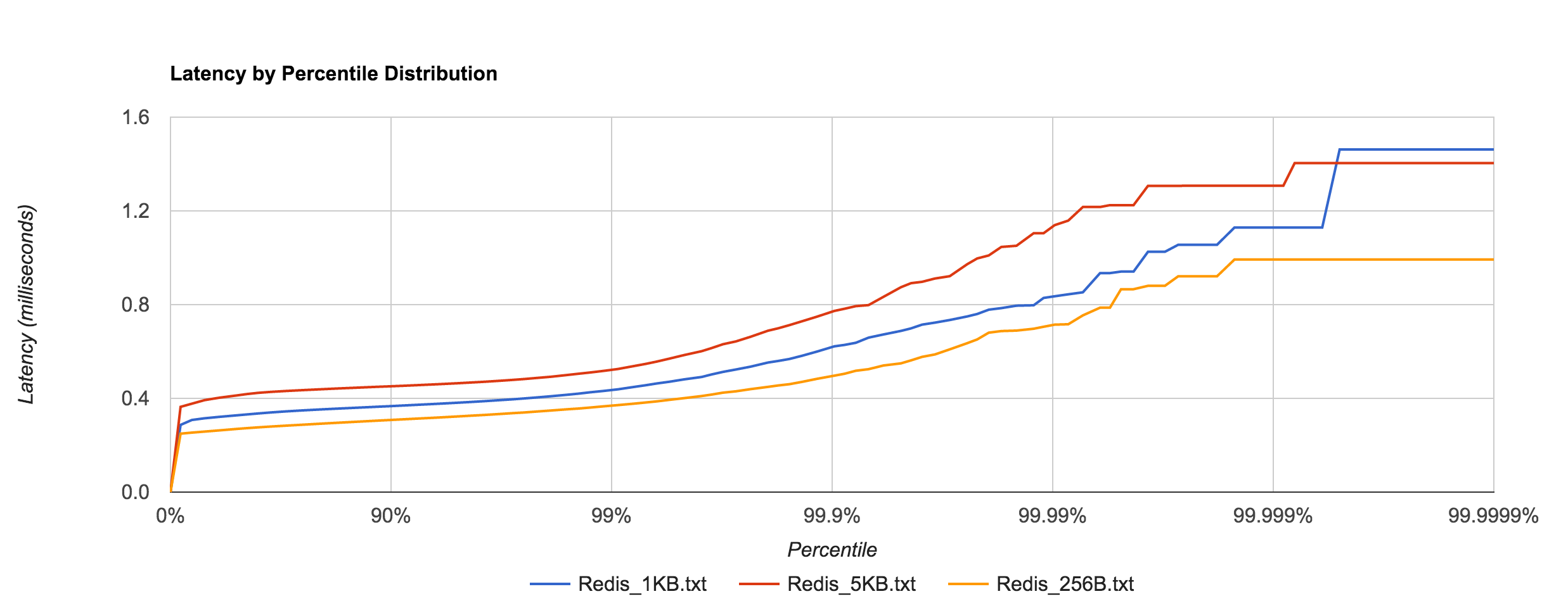
Redis tail latency peaks around 1.5 ms.

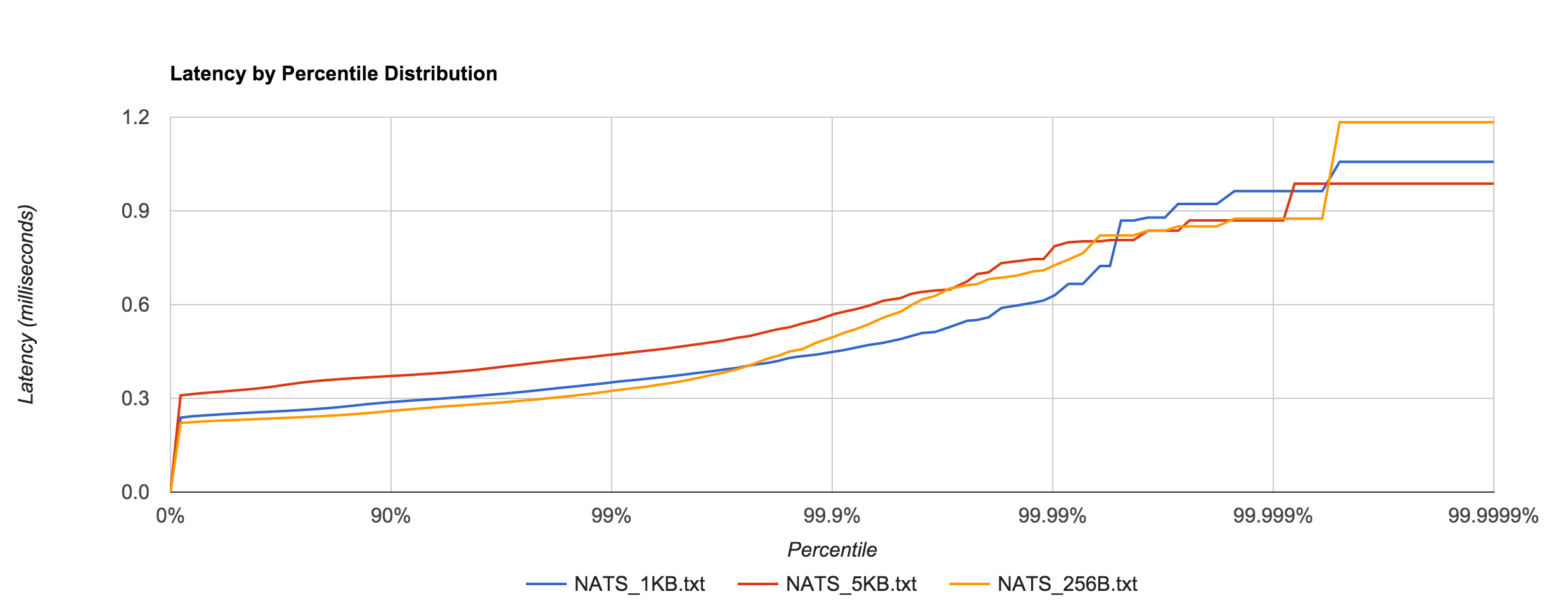
NATS performance looks comparable to Redis. Latency peaks around 1.2 ms.

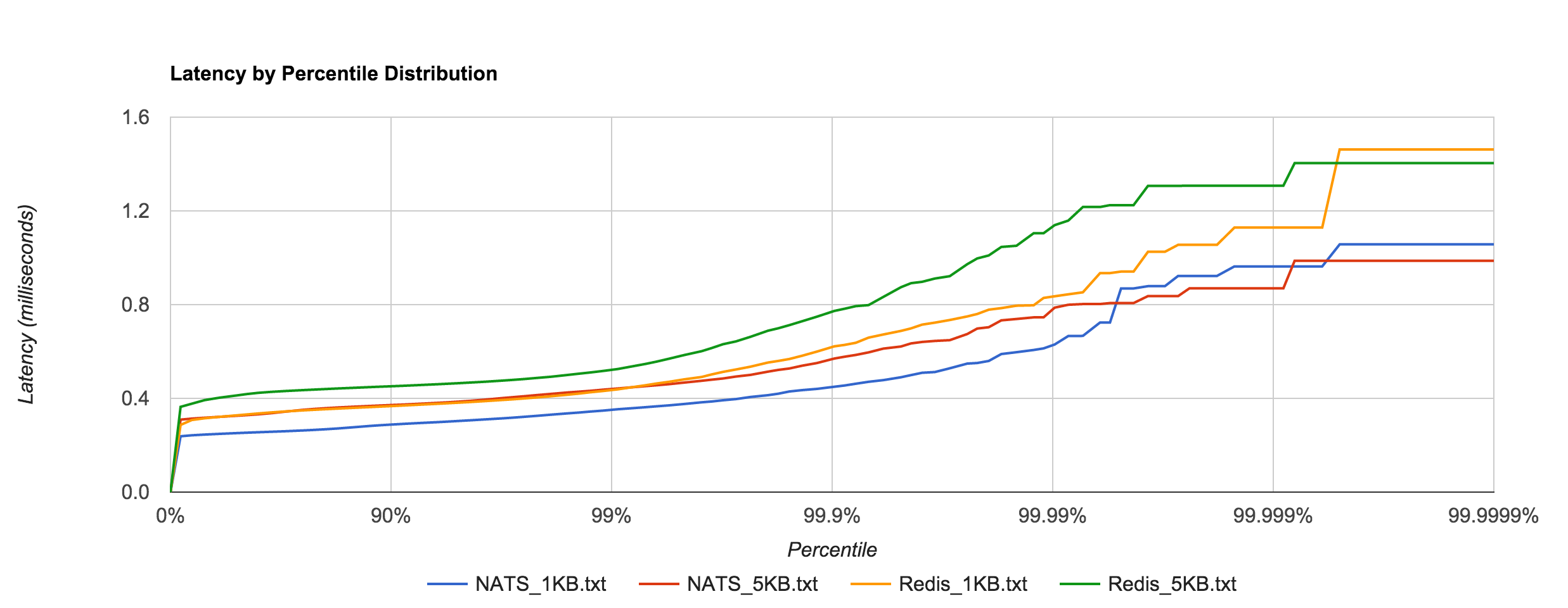
The resemblance becomes more apparent when we overlay the two distributions for the 1KB and 5KB runs. NATS tends to be about 0.1 to 0.4 ms faster.

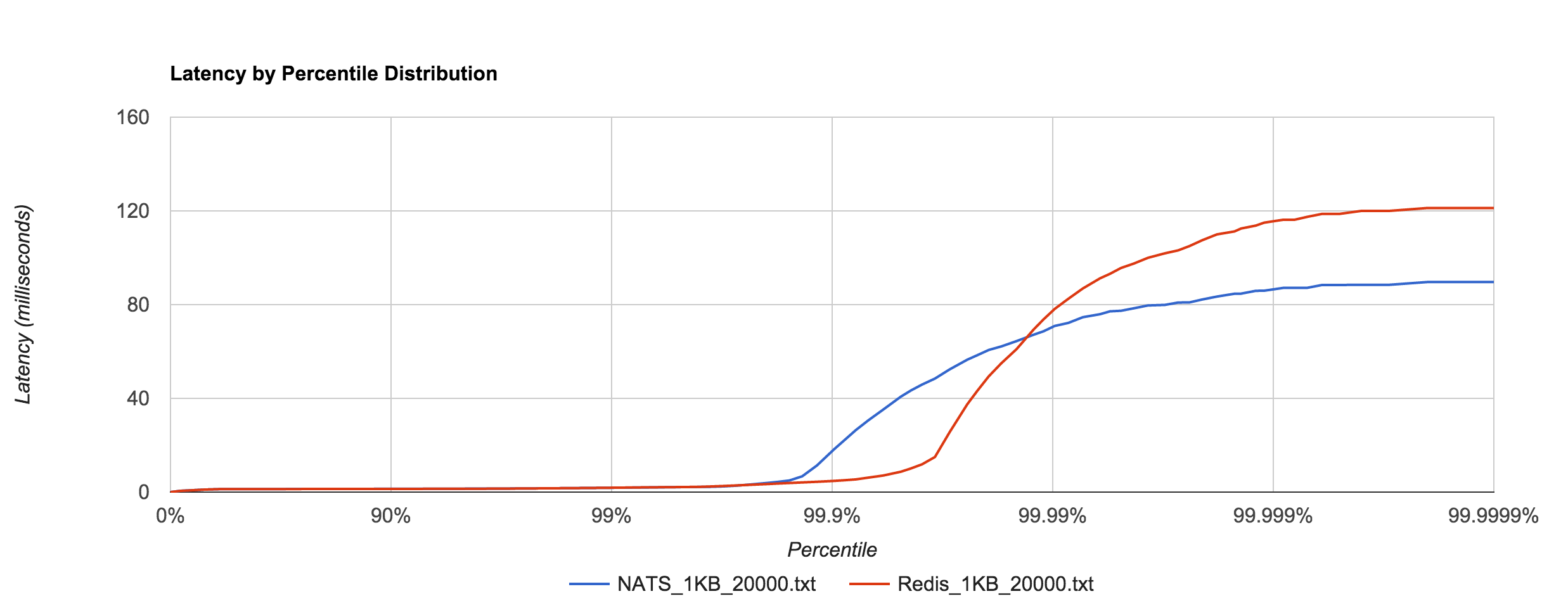
The 1KB, 20,000 requests/sec run uses 25 concurrent connections. With concurrent load, tail latencies jump up, peaking around 90 and 120 ms at the 99.9999th percentile in NATS and Redis, respectively.

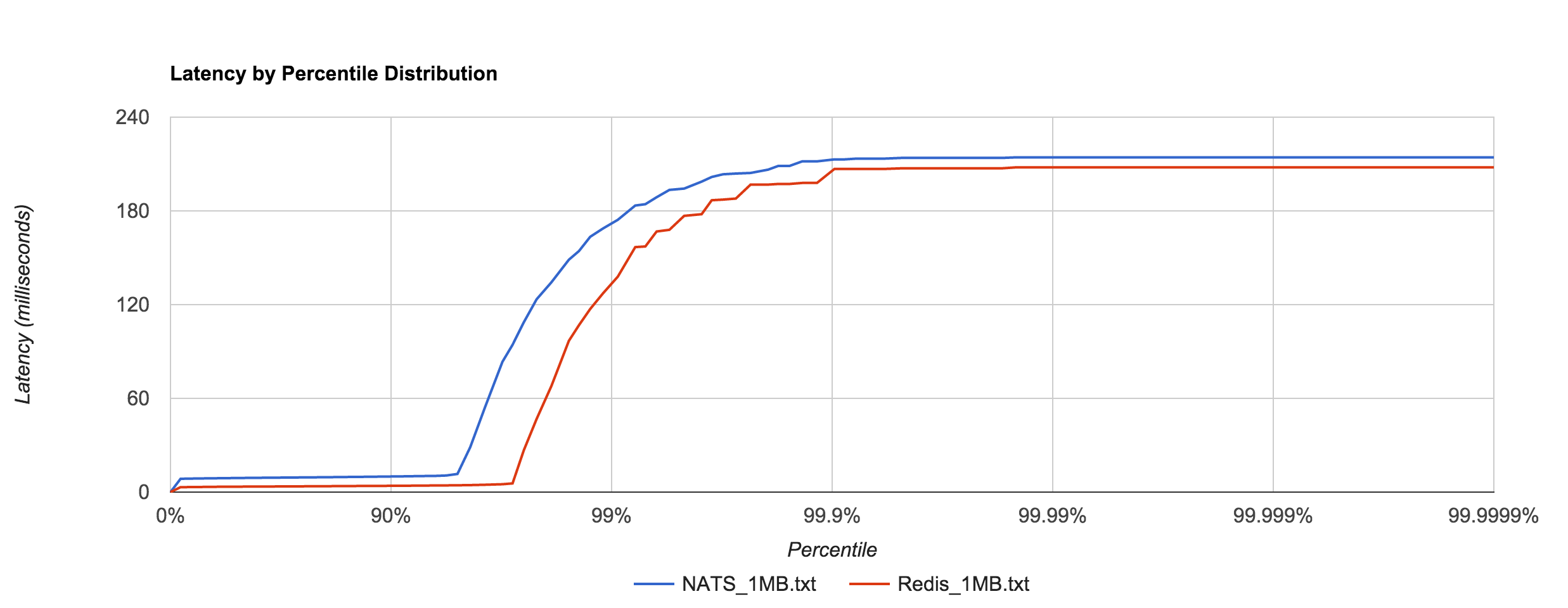
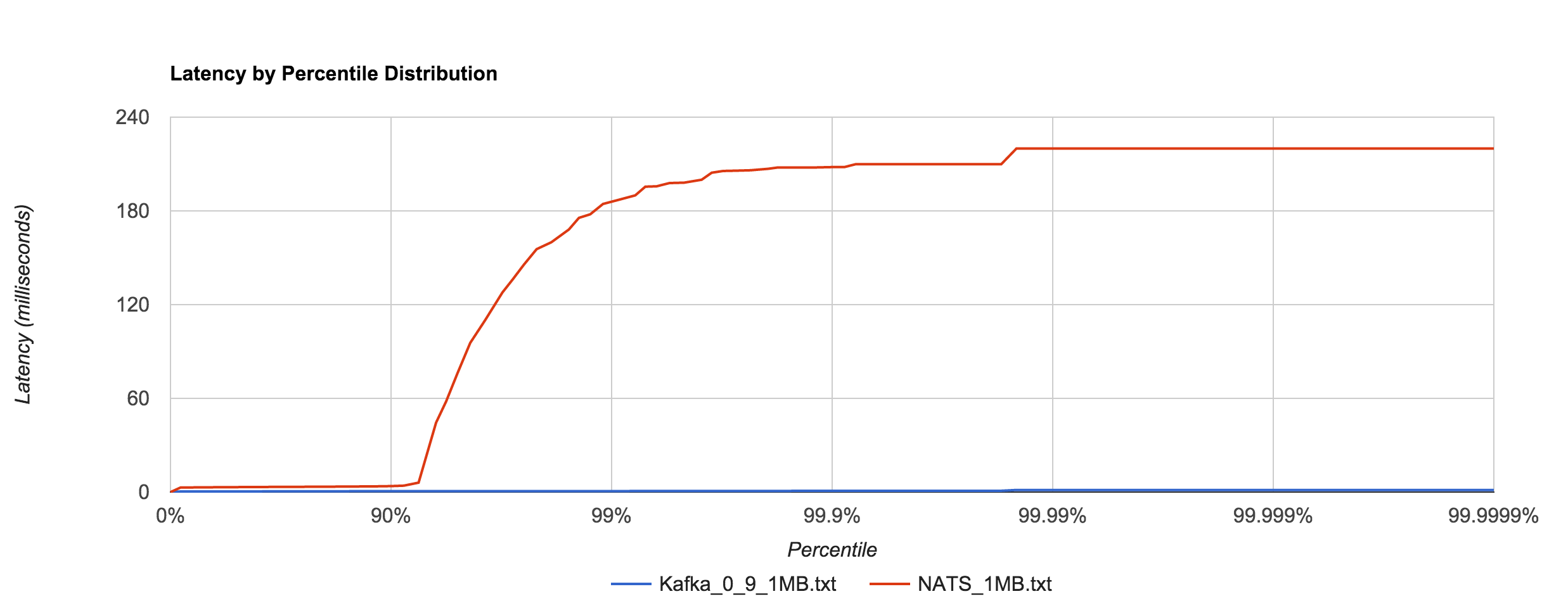
Large messages (1MB) don’t hold up nearly as well, exhibiting large tail latencies starting around the 95th and 97th percentiles in NATS and Redis, respectively. 1MB is the default maximum message size in NATS. The latency peaks around 214 ms. Again, keep in mind these are synchronous, roundtrip latencies.

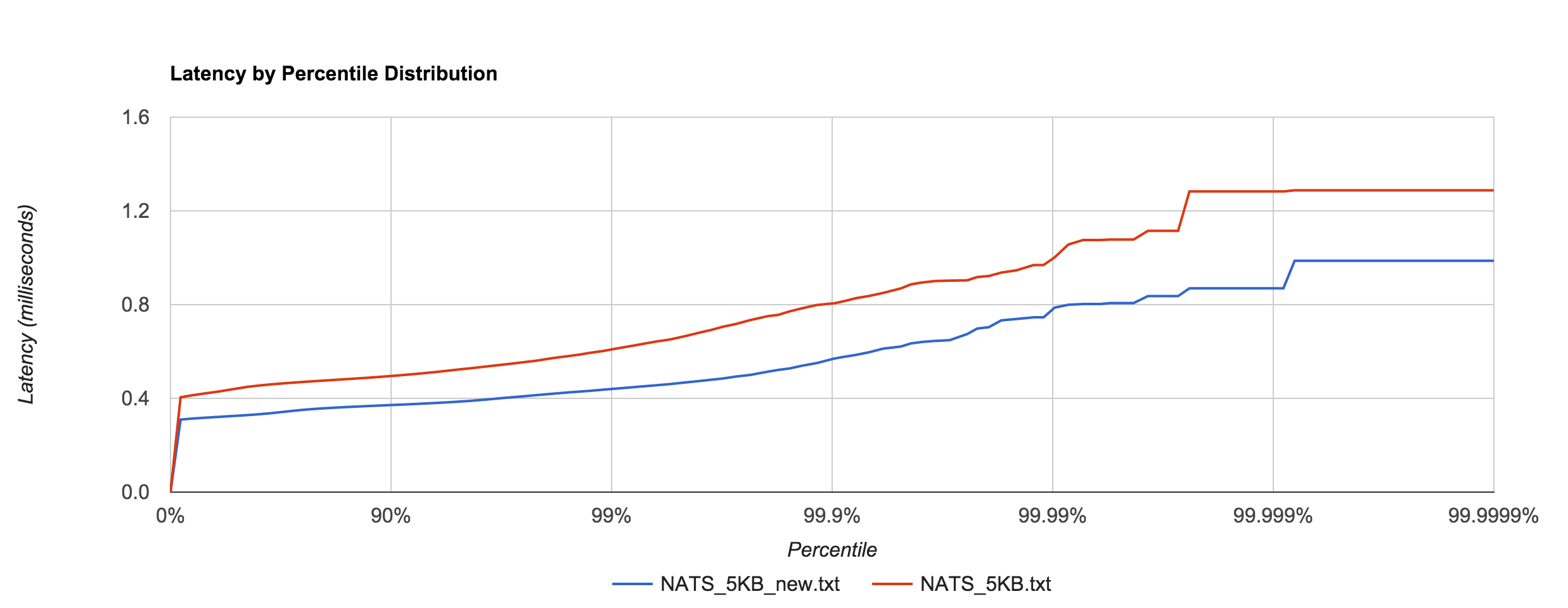
Apcera’s Ivan Kozlovic pointed out that the version of the NATS client I was using didn’t include a recent performance optimization. Before, the protocol parser scanned over each byte in the payload, but the newer version skips to the end (the previous benchmarks were updated to use the newer version). The optimization does have a noticeable effect, illustrated below. There was about a 30% improvement with the 5KB latencies.

The difference is even more pronounced in the 1MB case, which has roughly a 90% improvement up to the 90th percentile. The linear scale in the graph below hides this fact, but at the 90th percentile, for example, the pre-optimization latency is 10 ms and the optimized latency is 3.8 ms. Clearly, the large tail is mostly unaffected, however.

In general, this shows that NATS and Redis are better suited to smaller messages (well below 1MB), in which latency tends to be sub-millisecond up to four nines.

RabbitMQ and Kafka

RabbitMQ is a popular AMQP implementation. Unlike NATS, it’s a more traditional message queue in the sense that it supports binding queues and transactional-delivery semantics. Consequently, RabbitMQ is a more “heavyweight” queuing solution and tends to pay an additional premium with latency. In this benchmark, non-durable queues were used. As a result, we should see reduced latencies since we aren’t going to disk.

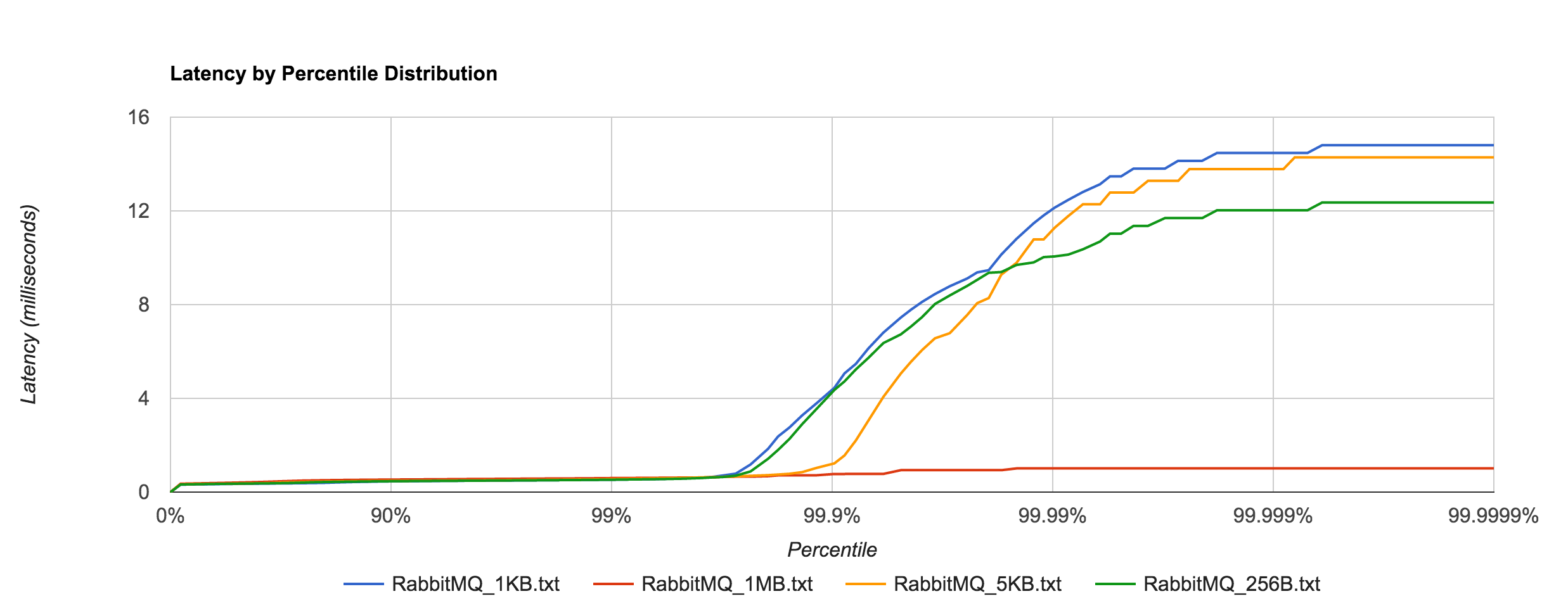
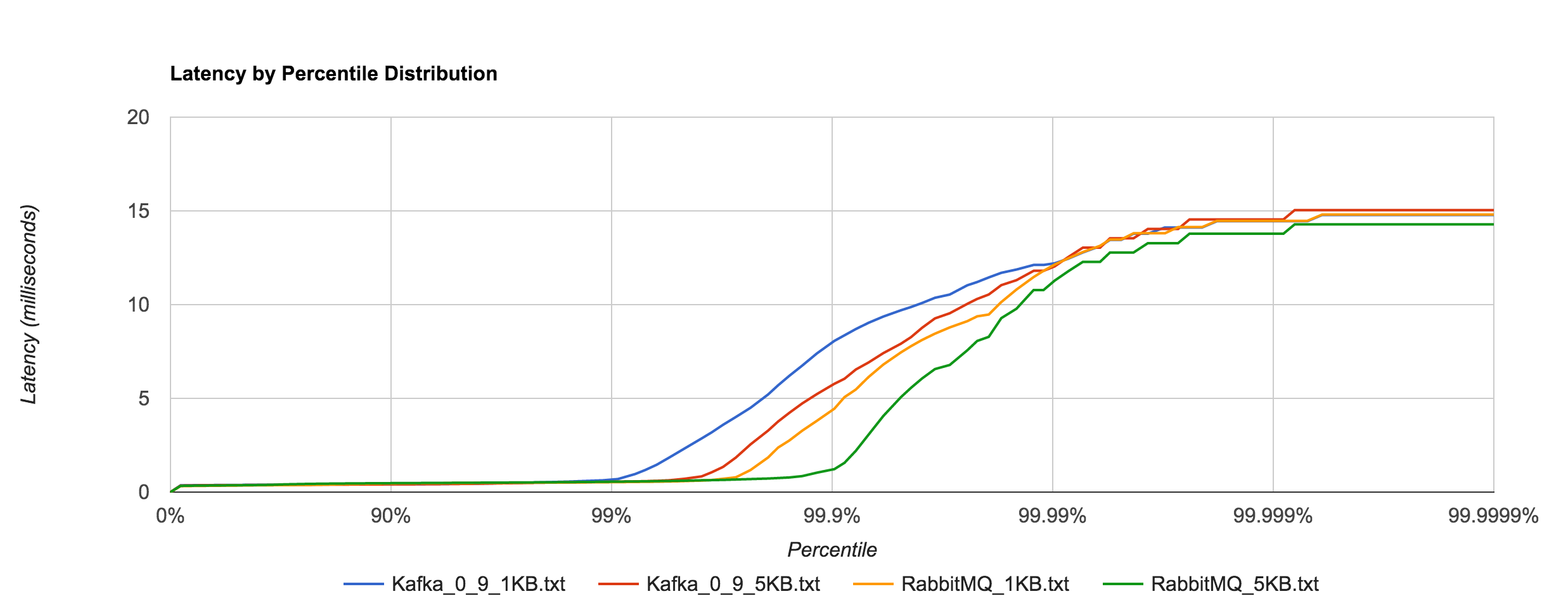
Latency tends to be sub-millisecond up to the 99.7th percentile, but we can see that it doesn’t hold up to NATS beyond that point for the 1KB and 5KB payloads.

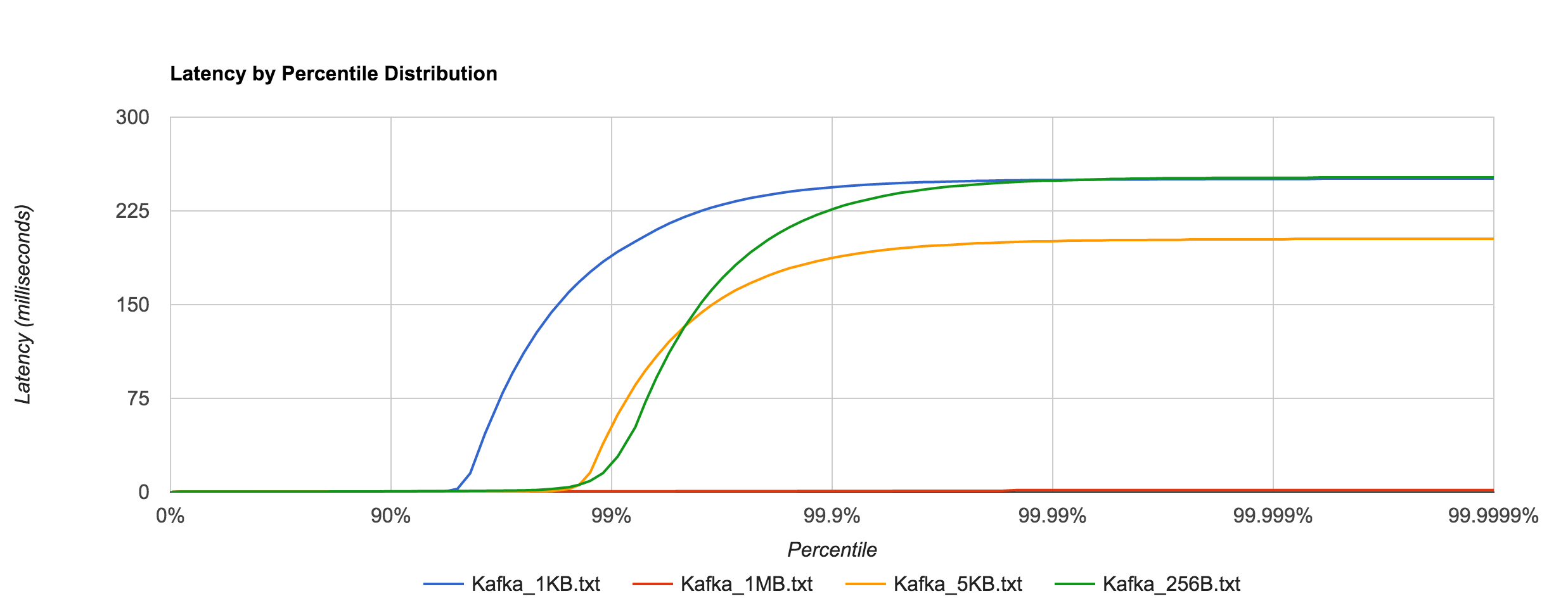
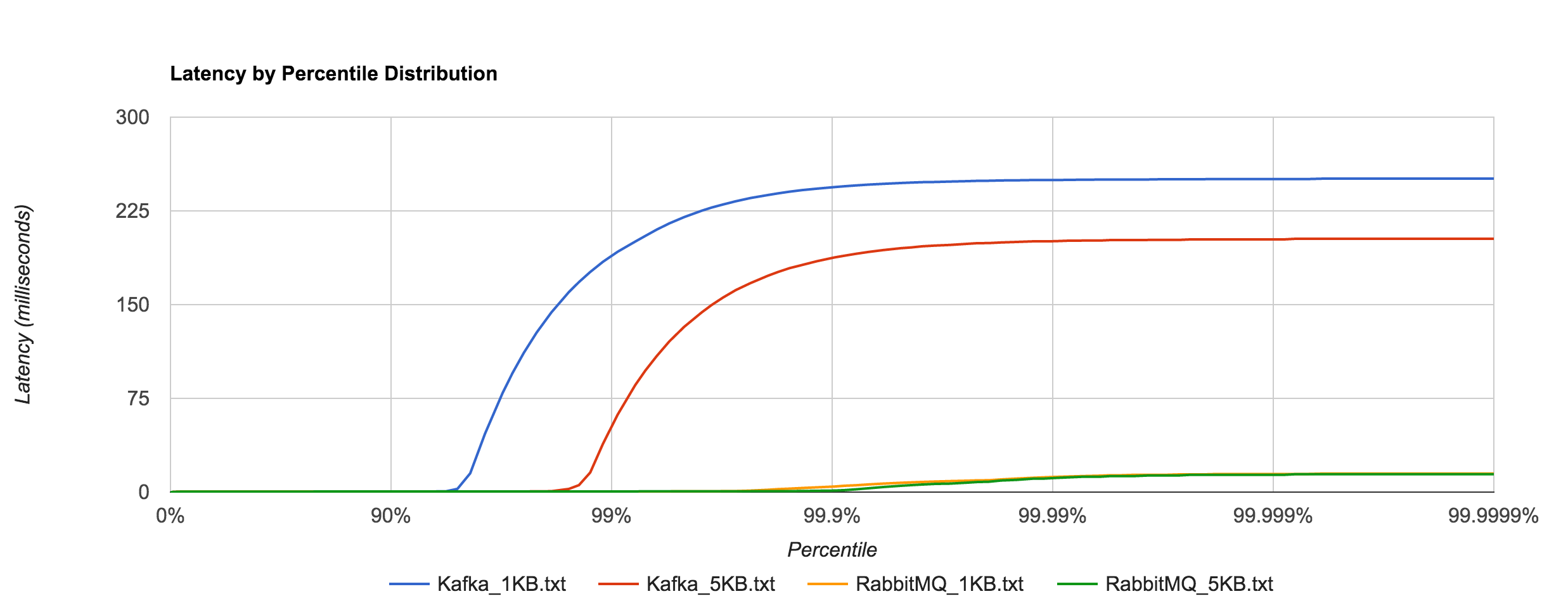
Kafka, on the other hand, requires disk persistence, but this doesn’t have a dramatic effect on latency until we look at the 94th percentile and beyond, when compared to RabbitMQ. Writes should be to page cache with flushes to disk happening asynchronously. The graphs below are for 0.8.2.2.

Once again, the 1KB, 20,000 requests/sec run is distributed across 25 concurrent connections. With RabbitMQ, we see the dramatic increase in tail latencies as we did with Redis and NATS. The RabbitMQ latencies in the concurrent case stay in line with the previous latencies up to about the 99th percentile. Interestingly, Kafka, doesn’t appear to be significantly affected. The latencies of 20,000 requests/sec at 1KB per request are not terribly different than the latencies of 3,000 requests/sec at 1KB per request, both peaking around 250 ms.

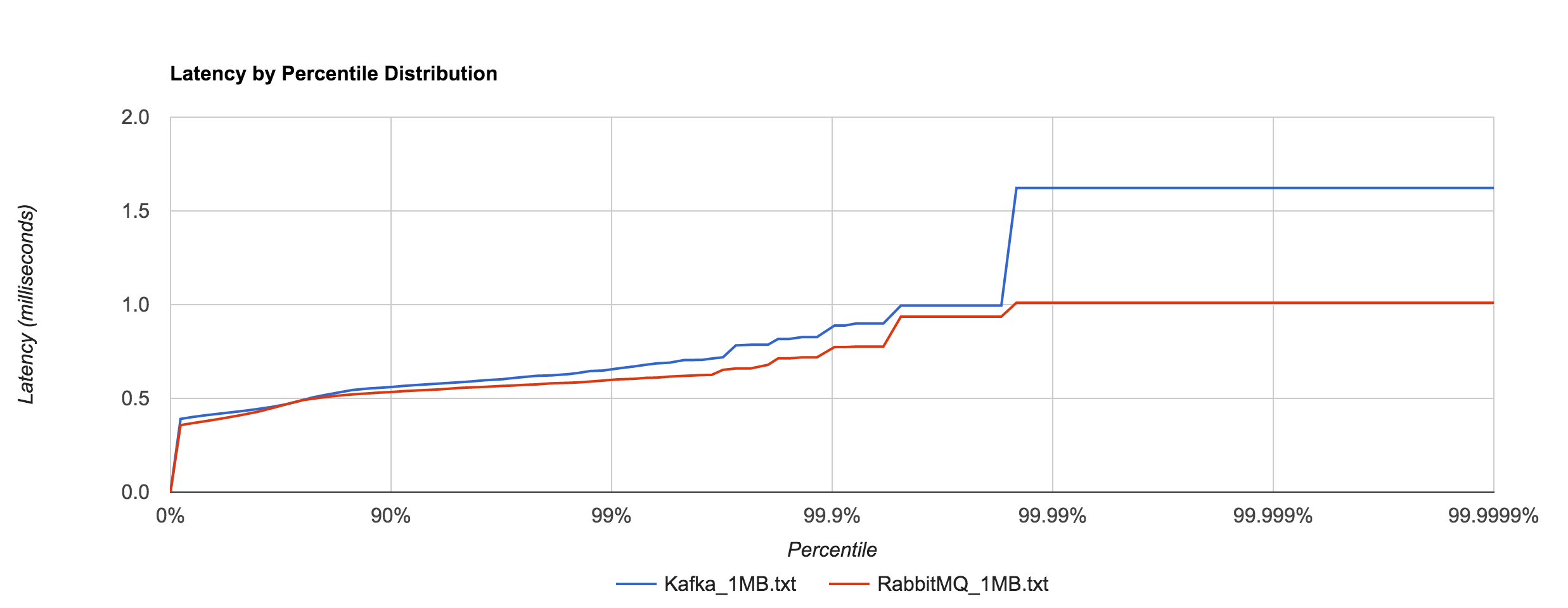
What’s particularly interesting is the behavior of 1MB messages vs. the rest. With RabbitMQ, there’s almost a 14x difference in max latencies between the 5KB and 1MB runs with 1MB being the faster. With Kafka 0.8.2.2, the difference is over 126x in the same direction. We can plot the 1MB latencies for RabbitMQ and Kafka since it’s difficult to discern them with a linear scale.

I tried to understand what was causing this behavior. I’ve yet to find a reasonable explanation for RabbitMQ. Intuition tells me it’s a result of buffering—either at the OS level or elsewhere—and the large messages cause more frequent flushing. Remember that these benchmarks were with transient publishes. There should be no disk accesses occurring, though my knowledge of Rabbit’s internals are admittedly limited. The fact that this behavior occurs in RabbitMQ and not Redis or NATS seems odd. Nagle’s algorithm is disabled in all of the benchmarks (TCP_NODELAY). After inspecting packets with Wireshark, it doesn’t appear to be a problem with delayed acks.

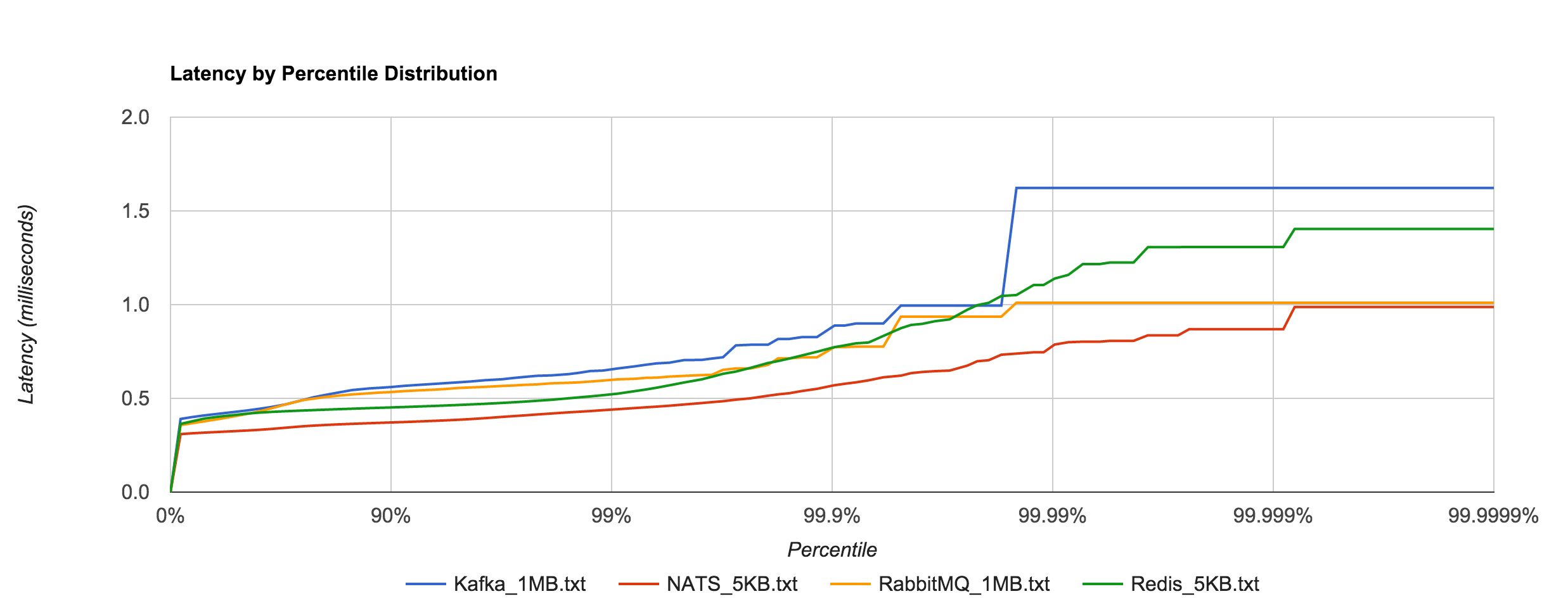
To show just how staggering the difference is, we can plot Kafka 0.8.2.2 and RabbitMQ 1MB latencies alongside Redis and NATS 5KB latencies. They are all within the same ballpark. Whatever the case may be, both RabbitMQ and Kafka appear to handle large messages extremely well in contrast to Redis and NATS.

This leads me to believe you’ll see better overall throughput, in terms of raw data, with RabbitMQ and Kafka, but more predictable, tighter tail latencies with Redis and NATS. Where SLAs are important, it’s hard to beat NATS. Of course, it’s unfair to compare Kafka with something like NATS or Redis or even RabbitMQ since they are very different (and sometimes complementary), but it’s also worth pointing out that the former is much more operationally complex.

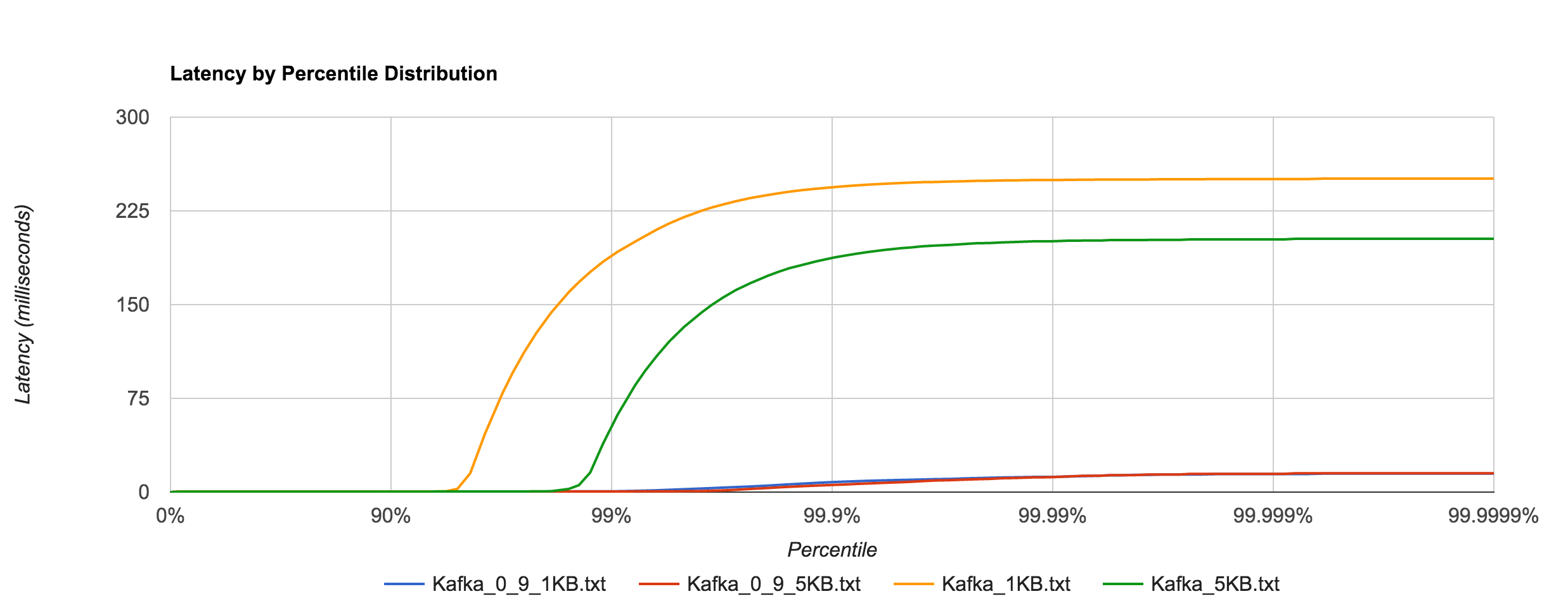
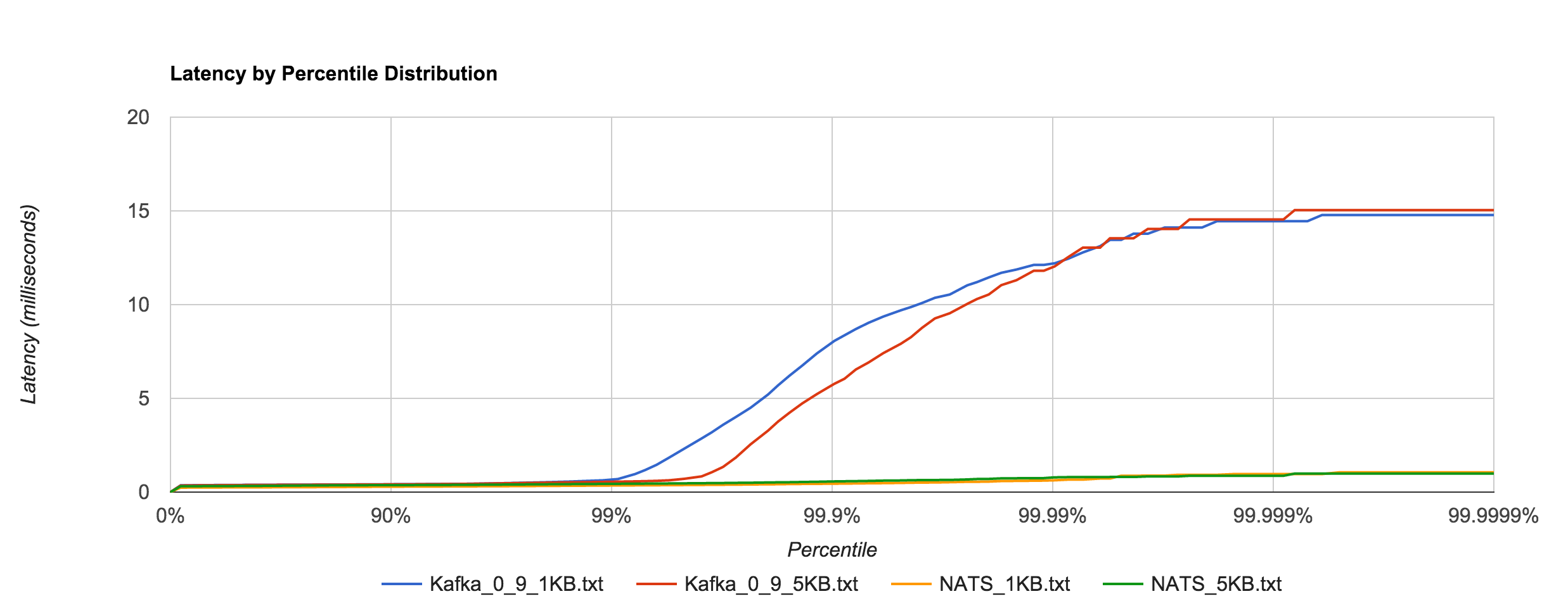
However, benchmarking Kafka 0.9.0.0 (blue and red) shows an astounding difference in tail latencies compared to 0.8.2.2 (orange and green).

Kafka 0.9’s performance is much more in line with RabbitMQ’s at high percentiles as seen below.

Likewise, it’s a much closer comparison to NATS when looking at the 1KB and 5KB runs.

As with 0.8, Kafka 0.9 does an impressive job dealing with 1MB messages in comparison to NATS, especially when looking at the 92nd percentile and beyond. It’s hard to decipher in the graph below, but Kafka 0.9’s 99th, 99.9th, and 99.99th percentile latencies are 0.66, 0.78, and 1.35 ms, respectively.

My initial thought was that the difference between Kafka 0.8 and 0.9 was attributed to a change in fsync behavior. To quote the Kafka documentation:

Kafka always immediately writes all data to the filesystem and supports the ability to configure the flush policy that controls when data is forced out of the OS cache and onto disk using the and flush. This flush policy can be controlled to force data to disk after a period of time or after a certain number of messages has been written.

However, there don’t appear to be any changes in the default flushing configuration between 0.8 and 0.9. The default configuration disables application fsync entirely, instead relying on the OS’s background flush. Jay Kreps indicates it’s a result of several “high percentile latency issues” that were fixed in 0.9. After scanning the 0.9 release notes, I was unable to determine specifically what those fixes might be. Either way, the difference is certainly not something to scoff at.

Conclusion

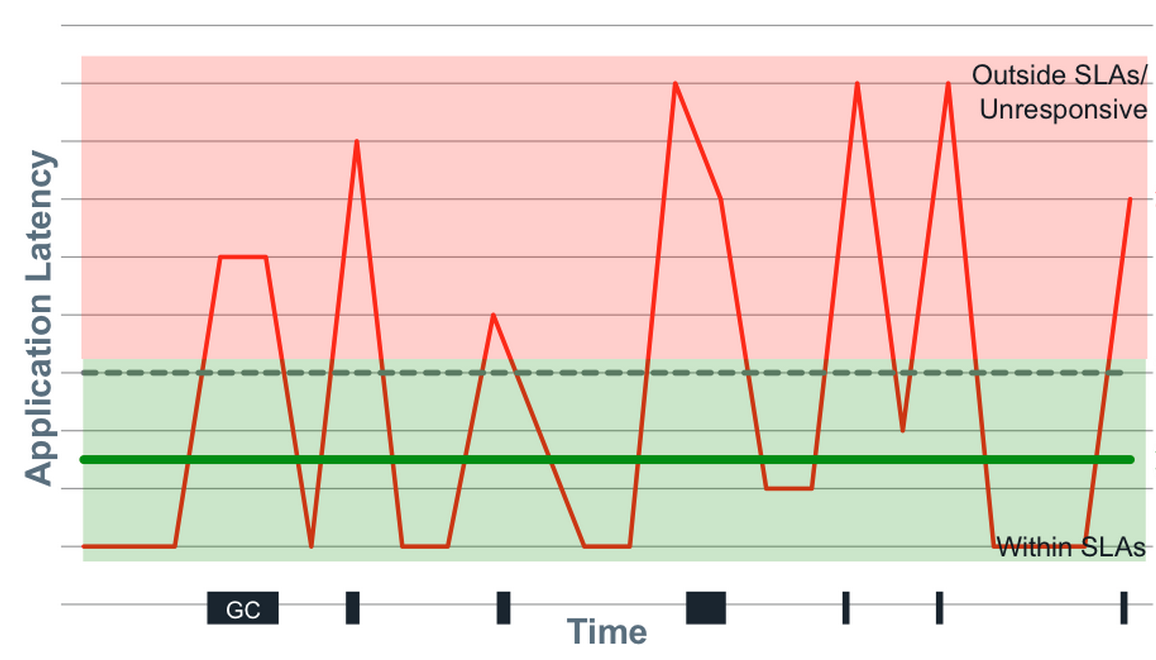
As always, interpret these benchmark results with a critical eye and perform your own tests if you’re evaluating these systems. This was more an exercise in benchmark methodology and tooling than an actual system analysis (and, as always, there’s still a lot of room for improvement). If anything, I think these results show how much we can miss by not looking beyond the 99th percentile. In almost all cases, everything looks pretty good up to that point, but after that things can get really bad. This is important to be conscious of when discussing SLAs.

I think the key takeaway is to consider your expected load in production, benchmark configurations around that, determine your allowable service levels, and iterate or provision more resources until you’re within those limits. The other important takeaway with respect to benchmarking is to look at the complete latency distribution. Otherwise, you’re not getting a clear picture of how your system actually behaves.

Follow @tyler_treat

December 12, 2015October 11, 2019

Everything You Know About Latency Is Wrong

Okay, maybe not everything you know about latency is wrong. But now that I have your attention, we can talk about why the tools and methodologies you use to measure and reason about latency are likely horribly flawed. In fact, they’re not just flawed, they’re probably lying to your face.

When I went to Strange Loop in September, I attended a workshop called “Understanding Latency and Application Responsiveness” by Gil Tene. Gil is the CTO of Azul Systems, which is most renowned for its C4 pauseless garbage collector and associated Zing Java runtime. While the workshop was four and a half hours long, Gil also gave a 40-minute talk called “How NOT to Measure Latency” which was basically an abbreviated, less interactive version of the workshop. If you ever get the opportunity to see Gil speak or attend his workshop, I recommend you do. At the very least, do yourself a favor and watch one of his recorded talks or find his slide decks online.

The remainder of this post is primarily a summarization of that talk. You may not get anything out of it that you wouldn’t get out of the talk, but I think it can be helpful to absorb some of these ideas in written form. Plus, for my own benefit, writing about them helps solidify it in my head.

What is Latency?

Latency is defined as the time it took one operation to happen. This means every operation has its own latency—with one million operations there are one million latencies. As a result, latency cannot be measured as work units / time. What we’re interested in is how latency behaves. To do this meaningfully, we must describe the complete distribution of latencies. Latency almost never follows a normal, Gaussian, or Poisson distribution, so looking at averages, medians, and even standard deviations is useless.

Latency tends to be heavily multi-modal, and part of this is attributed to “hiccups” in response time. Hiccups resemble periodic freezes and can be due to any number of reasons—GC pauses, hypervisor pauses, context switches, interrupts, database reindexing, cache buffer flushes to disk, etc. These hiccups never resemble normal distributions and the shift between modes is often rapid and eclectic.

Screen Shot 2015-10-04 at 4.32.24 PM

How do we meaningfully describe the distribution of latencies? We have to look at percentiles, but it’s even more nuanced than this. A trap that many people fall into is fixating on “the common case.” The problem with this is that there is a lot more to latency behavior than the common case. Not only that, but the “common” case is likely not as common as you think.

This is partly a tooling problem. Many of the tools we use do not do a good job of capturing and representing this data. For example, the majority of latency graphs produced by Grafana, such as the one below, are basically worthless. We like to look at pretty charts, and by plotting what’s convenient we get a nice colorful graph which is quite readable. Only looking at the 95th percentile is what you do when you want to hide all the bad stuff. As Gil describes, it’s a “marketing system.” Whether it’s the CTO, potential customers, or engineers—someone’s getting duped. Furthermore, averaging percentiles is mathematically absurd. To conserve space, we often keep the summaries and throw away the data, but the “average of the 95th percentile” is a meaningless statement. You cannot average percentiles, yet note the labels in most of your Grafana charts. Unfortunately, it only gets worse from here.

graph_logbase10_ms

Gil says, “The number one indicator you should never get rid of is the maximum value. That is not noise, that is the signal. The rest of it is noise.” To this point, someone in the workshop naturally responded with “But what if the max is just something like a VM restarting? That doesn’t describe the behavior of the system. It’s just an unfortunate, unlikely occurrence.” By ignoring the maximum, you’re effectively saying “this doesn’t happen.” If you can identify the cause as noise, you’re okay, but if you’re not capturing that data, you have no idea of what’s actually happening.

How Many Nines?

But how many “nines” do I really need to look at? The 99th percentile, by definition, is the latency below which 99% of the observations may be found. Is the 99th percentile rare? If we have a single search engine node, a single key-value store node, a single database node, or a single CDN node, what is the chance we actually hit the 99th percentile?

Gil describes some real-world data he collected which shows how many of the web pages we go to actually experience the 99th percentile, displayed in table below. The second column counts the number of HTTP requests generated by a single access of the web page. The third column shows the likelihood of one access experiencing the 99th percentile. With the exception of google.com, every page has a probability of 50% or higher of seeing the 99th percentile.

Screen Shot 2015-10-04 at 6.15.24 PM

The point Gil makes is that the 99th percentile is what most of your web pages will see. It’s not “rare.”

What metric is more representative of user experience? We know it’s not the average or the median. 95th percentile? 99.9th percentile? Gil walks through a simple, hypothetical example: a typical user session involves five page loads, averaging 40 resources per page. How many users will not experience something worse than the 95th percentile? 0.003%. By looking at the 95th percentile, you’re looking at a number which is relevant to 0.003% of your users. This means 99.997% of your users are going to see worse than this number, so why are you even looking at it?

On the flip side, 18% of your users are going to experience a response time worse than the 99.9th percentile, meaning 82% of users will experience the 99.9th percentile or better. Going further, more than 95% of users will experience the 99.97th percentile and more than 99% of users will experience the 99.995th percentile.

The median is the number that 99.9999999999% of response times will be worse than. This is why median latency is irrelevant. People often describe “typical” response time using a median, but the median just describes what everything will be worse than. It’s also the most commonly used metric.

If it’s so critical that we look at a lot of nines (and it is), why do most monitoring systems stop at the 95th or 99th percentile? The answer is simply because “it’s hard!” The data collected by most monitoring systems is usually summarized in small, five or ten second windows. This, combined with the fact that we can’t average percentiles or derive five nines from a bunch of small samples of percentiles means there’s no way to know what the 99.999th percentile for the minute or hour was. We end up throwing away a lot of good data and losing fidelity.

A Coordinated Conspiracy

Benchmarking is hard. Almost all latency benchmarks are broken because almost all benchmarking tools are broken. The number one cause of problems in benchmarks is something called “coordinated omission,” which Gil refers to as “a conspiracy we’re all a part of” because it’s everywhere. Almost all load generators have this problem.

We can look at a common load-testing example to see how this problem manifests. With this type of test, a client generally issues requests at a certain rate, measures the response time for each request, and puts them in buckets from which we can study percentiles later.

The problem is what if the thing being measured took longer than the time it would have taken before sending the next thing? What if you’re sending something every second, but this particular thing took 1.5 seconds? You wait before you send the next one, but by doing this, you avoided measuring something when the system was problematic. You’ve coordinated with it by backing off and not measuring when things were bad. To remain accurate, this method of measuring only works if all responses fit within an expected interval.

Coordinated omission also occurs in monitoring code. The way we typically measure something is by recording the time before, running the thing, then recording the time after and looking at the delta. We put the deltas in stats buckets and calculate percentiles from that. The code below is taken from a Cassandra benchmark.

Screen Shot 2015-10-04 at 7.29.09 PM

However, if the system experiences one of the “hiccups” described earlier, you will only have one bad operation and 10,000 other operations waiting in line. When those 10,000 other things go through, they will look really good when in reality the experience was really bad. Long operations only get measured once, and delays outside the timing window don’t get measured at all.

In both of these examples, we’re omitting data that looks bad on a very selective basis, but just how much of an impact can this have on benchmark results? It turns out the impact is huge.

Screen Shot 2015-10-04 at 7.27.43 PM

Imagine a “perfect” system which processes 100 requests/second at exactly 1 ms per request. Now consider what happens when we freeze the system (for example, using CTRL+Z) after 100 seconds of perfect operation for 100 seconds and repeat. We can intuitively characterize this system:

The average over the first 100 seconds is 1 ms.
The average over the next 100 seconds is 50 seconds.
The average over the 200 seconds is 25 seconds.
The 50th percentile is 1 ms.
The 75th percentile is 50 seconds.
The 99.99th percentile is 100 seconds.

Screen Shot 2015-10-04 at 7.49.10 PM

Now we try measuring the system using a load generator. Before freezing, we run 100 seconds at 100 requests/second for a total of 10,000 requests at 1 ms each. After the stall, we get one result of 100 seconds. This is the entirety of our data, and when we do the math, we get these results:

The average over the 200 seconds is 10.9 ms (should be 25 seconds).
The 50th percentile is 1 ms.
The 75th percentile is 1 ms (should be 50 seconds).
The 99.99th percentile is 1 ms (should be 100 seconds).

Screen Shot 2015-10-04 at 7.57.23 PM

Basically, your load generator and monitoring code tell you the system is ready for production, when in fact it’s lying to you! A simple “CTRL+Z” test can catch coordinated omission, but people rarely do it. It’s critical to calibrate your system this way. If you find it giving you these kind of results, throw away all the numbers—they’re worthless.

You have to measure at random or “fair” rates. If you measure 10,000 things in the first 100 seconds, you have to measure 10,000 things in the second 100 seconds during the stall. If you do this, you’ll get the correct numbers, but they won’t be as pretty. Coordinated omission is the simple act of erasing, ignoring, or missing all the “bad” stuff, but the data is good.

Surely this data can still be useful though, even if it doesn’t accurately represent the system? For example, we can still use it to identify performance regressions or validate improvements, right? Sadly, this couldn’t be further from the truth. To see why, imagine we improve our system. Instead of pausing for 100 seconds after 100 seconds of perfect operation, it handles all requests at 5 ms each after 100 seconds. Doing the math, we get the following:

The 50th percentile is 1 ms
The 75th percentile is 2.5 ms (stall showed 1 ms)
The 99.99th percentile is 5 ms (stall showed 1 ms)

This data tells us we hurt the four nines and made the system 5x worse! This would tell us to revert the change and go back to the way it was before, which is clearly the wrong decision. With bad data, better can look worse. This shows that you cannot have any intuition based on any of these numbers. The data is garbage.

With many load generators, the situation is actually much worse than this. These systems work by generating a constant load. If our test is generating 100 requests/second, we run 10,000 requests in the first 100 seconds. When we stall, we process just one request. After the stall, the load generator sees that it’s 9,999 requests behind and issues those requests to catch back up. Not only did it get rid of the bad requests, it replaced them with good requests. Now the data is twice as wrong as just dropping the bad requests.

What coordinated omission is really showing you is service time, not response time. If we imagine a cashier ringing up customers, the service time is the time it takes the cashier to do the work. The response time is the time a customer waits before they reach the register. If the rate of arrival is higher than the service rate, the response time will continue to grow. Because hiccups and other phenomena happen, response times often bounce around. However, coordinated omission lies to you about response time by actually telling you the service time and hiding the fact that things stalled or waited in line.

Measuring Latency

Latency doesn’t live in a vacuum. Measuring response time is important, but you need to look at it in the context of load. But how do we properly measure this? When you’re nearly idle, things are nearly perfect, so obviously that’s not very useful. When you’re pedal to the metal, things fall apart. This is somewhat useful because it tells us how “fast” we can go before we start getting angry phone calls.

However, studying the behavior of latency at saturation is like looking at the shape of your car’s bumper after wrapping it around a pole. The only thing that matters when you hit the pole is that you hit the pole. There’s no point in trying to engineer a better bumper, but we can engineer for the speed at which we lose control. Everything is going to suck at saturation, so it’s not super useful to look at beyond determining your operating range.

What’s more important is testing the speeds in between idle and hitting the pole. Define your SLAs and plot those requirements, then run different scenarios using different loads and different configurations. This tells us if we’re meeting our SLAs but also how many machines we need to provision to do so. If you don’t do this, you don’t know how many machines you need.

How do we capture this data? In an ideal world, we could store information for every request, but this usually isn’t practical. HdrHistogram is a tool which allows you to capture latency and retain high resolution. It also includes facilities for correcting coordinated omission and plotting latency distributions. The original version of HdrHistogram was written in Java, but there are versions for many other languages.

Screen Shot 2015-10-05 at 12.00.04 AM

To Summarize

To understand latency, you have to consider the entire distribution. Do this by plotting the latency distribution curve. Simply looking at the 95th or even 99th percentile is not sufficient. Tail latency matters. Worse yet, the median is not representative of the “common” case, the average even less so. There is no single metric which defines the behavior of latency. Be conscious of your monitoring and benchmarking tools and the data they report. You can’t average percentiles.

Remember that latency is not service time. If you plot your data with coordinated omission, there’s often a quick, high rise in the curve. Run a “CTRL+Z” test to see if you have this problem. A non-omitted test has a much smoother curve. Very few tools actually correct for coordinated omission.

Latency needs to be measured in the context of load, but constantly running your car into a pole in every test is not useful. This isn’t how you’re running in production, and if it is, you probably need to provision more machines. Use it to establish your limits and test the sustainable throughputs in between to determine if you’re meeting your SLAs. There are a lot of flawed tools out there, but HdrHistogram is one of the few that isn’t. It’s useful for benchmarking and, since histograms are additive and HdrHistogram uses log buckets, it can also be useful for capturing high-volume data in production.

Follow @tyler_treat